Generative Adversarial Nets

李沐精读论文：

《花书》作者Goodfellow 等人于2014年提出了GAN打开了绚丽多彩的博弈生成模型的大门，GAN的核心思想就是博弈论的相互对抗，纳什均衡：其思想主要构造两个深度神经网络：判别器D和生成器G，为GAN提供一些真实钞票作为训练样本，生成器G生成假的钞票来欺骗判别器D，给定一张钞票判别器D判断是否来自真币还是G生成的假币。判别器和生成器交替训练，相互提高，最终使得判别器D无法区分钞票的真假，生成器G就能生成如假包换的钞票糊弄判别器。

Ian J. Goodfellow（《花书》作者）∗, Jean Pouget-Abadie†, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair‡, Aaron Courville, Yoshua Bengio

核心思想：对抗博弈、纳什均衡

小虎AI珏爷：Transformer -基于BERT微调阅读理解问答模型实战

小虎AI珏爷：论文阅读：T5 用统一的文本到文本Transformer探索迁移学习的局限性（金钱屠榜）2019

实战基于BERT微调实现MRC阅读理解问答系统：小虎AI珏爷：Transformer -基于BERT微调阅读理解问答模型实战

小虎AI珏爷：论文阅读：知识库问答自动生成 Info-HCVAE(ACL 2020)

小虎AI珏爷：论文阅读：通过生成性预训练提高自然语言理解（GPT 2018）

小虎AI珏爷：基于知识库使用预训练模型构建抽取式（MRC-QA）以及生成式问答系统（BM25、BERT、GPT、T5）

小虎AI珏爷：论文阅读：GANs N’ Roses: Stable, Controllable, Diverse Image to Image Translation (works for videos too!)

摘要

论文提出了一个通过对抗过程估计生成模型的新框架，其中我们同时训练两个模型：捕获数据分布的生成模型G和估计样本来自训练数据而非G的概率的判别模型D。G的训练过程是最大化D出错的概率。这个框架对应于一个最大最小的两人博弈游戏。在任意函数G和D的空间中，存在一个唯一的解，其中G恢复训练数据分布，D处处等于 1/2 。在G和D由多层感知机定义的情况下，整个系统可以通过反向传播进行训练。在训练或生成样本期间，不需要任何马尔可夫链或展开的近似推理网络。通过对生成的样本进行定性和定量评估，实验证明了该框架的潜力。

1. 介绍

深度学习的前景是发现丰富的层次模型，这些模型代表人工智能应用中遇到的各种数据的概率分布，例如自然图像、包含语音的音频波形和自然语言语料库中的符号。到目前为止，深度学习中最显著的成功涉及到辨别模型，通常是那些将高维、丰富的感官输入映射到类别标签的模型。这些惊人的成功主要是基于反向传播和dropout算法，使用分段线性单元，具有特别好的梯度。深度生成模型的影响较小，这是因为很难对最大似然估计和相关策略中出现的许多难以处理的概率计算进行近似，以及很难在生成环境中利用分段线性单元的优点。论文提出了一种新的生成模型估计方法，以避免这些困难。

在提出的对抗性网络框架中，一个是判别模型，用于学习确定样本是来自模型分布还是数据分布。另一个是生成模型，生成模型可以被认为类似于一组伪造者，试图制造假币并在未被发现的情况下使用它，而判别模型类似于警察，试图检测假币。他们不断进行博弈。

该框架可以为多种模型和优化算法生成特定的训练算法。在本文中，论文探讨了生成模型通过多层感知器传递随机噪声来生成样本的特殊情况，而判别模型也是多层感知器。论文把这种特殊情况称为对抗网。在这种情况下，可以仅使用非常成功的反向传播和dropout算法来训练这两个模型，并仅使用正向传播从生成模型中采样。不需要近似推理或马尔可夫链。

2. 相关工作

直到最近，关于深层生成模型的大多数工作都集中在提供概率分布函数参数说明的模型上。然后，可以通过最大对数似然来训练模型。在这个模型家族中，最成功的可能是深层玻尔兹曼机。此类模型通常具有难以处理的似然函数，因此需要对似然梯度进行多次近似。这些困难推动了“生成机”的发展，即模型不能明确表示可能性，但能够从所需的分布中生成样本。生成型随机网络是生成机的一个例子，它可以通过精确的反向传播而不是波尔兹曼机器所需的大量近似值进行训练。这项工作通过消除生成随机网络中使用的马尔可夫链，扩展了生成机的概念。

论文的工作通过生成过程反向传播导数，通过观察

$\lim _{\sigma \rightarrow 0} \nabla_{\boldsymbol{x}} \mathbb{E}_{\epsilon \sim \mathcal{N}\left(0, \sigma^{2} \boldsymbol{I}\right)} f(\boldsymbol{x}+\epsilon)=\nabla_{\boldsymbol{x}} f(\boldsymbol{x})\\$

在开展这项工作时，论文还不知道Kingma和Welling以及Rezende等人已经开发了更一般的随机反向传播规则，允许通过具有有限方差的高斯分布进行反向传播，并反向传播到协方差参数和平均值。这些反向传播规则可以让我们学习生成器的条件方差，我们在这项工作中将其视为超参数。Kingma和Welling以及Rezende等人【2使用随机反向传播来训练变分自编码器（VAE）。与生成对抗网络一样，变分自动编码器将一个可微生成网络与另一个神经网络配对。与生成性对抗网络不同，VAE中的第二个网络是执行近似推理的识别模型。GAN需要通过可见单元进行微分，因此无法对离散数据进行建模，而VAE需要通过隐藏单元进行微分，因此无法具有离散的潜在变量。

之前的工作也采用了使用判别标准来训练生成模型的方法。这些方法使用的标准对于深层生成模型来说是难以解决的。这些方法甚至很难对深层模型进行近似，因为它们涉及概率比，而概率比不能用概率下限的变分近似来近似。噪声对比估计（NCE）涉及通过学习权重来训练生成模型，使该模型有助于区分固定噪声分布中的数据。使用先前训练的模型作为噪声分布，可以训练一系列质量更高的模型。这可以被视为一种非正式的竞争机制，类似于对抗性网络游戏中使用的正式竞争。NCE的关键限制在于其“鉴别器”由噪声分布的概率密度与模式的比率定义。

有两个神经网络的概念已经被使用。最相关的工作是可预测性最小化。在可预测性最小化中，神经网络中的每个隐藏单元都被训练为不同于第二个网络的输出，第二个网络根据所有其他隐藏单元的值预测该隐藏单元的值。这项工作在三个重要方面不同于可预测性最小化：1）在这项工作中，网络之间的竞争是唯一的训练标准，并且其本身足以训练网络。2）比赛的性质是不同的。在可预测性最小化中，比较两个网络的输出，一个网络试图使输出相似，另一个网络试图使输出不同。所讨论的输出是单个标量。在GANs中，一个网络产生一个丰富的高维向量，用作另一个网络的输入，并尝试选择另一个网络不知道如何处理的输入。3）学习过程的规范是不同的。可预测性最小化被描述为一个目标函数最小化的优化问题，学习接近目标函数的最小值。GAN基于极大极小博弈而非优化问题，具有一个价值函数，一个代理寻求最大化，另一个寻求最小化。游戏在一个鞍点终止，该鞍点是一个玩家策略的最小值，另一个玩家策略的最大值。

生成对抗性网络有时会与“对抗样本”的相关概念相混淆。对抗样本是通过直接对分类网络的输入使用基于梯度的优化来找到的示例，以便找到与错误分类的数据相似的示例。这与目前的工作不同，因为对抗样本不是训练生成模型的机制。相反，对抗样本主要是一种分析工具，用于显示神经网络以有趣的方式进行行为，通常自信地以高置信度对两幅图像进行不同的分类，即使人类观察者无法察觉它们之间的差异。这种对抗样本的存在确实表明，生成性对抗性网络训练可能效率低下，因为它们表明，现代歧视性网络可以自信地识别一个阶级，而不模仿该阶级的任何人类可感知属性。

3. 对抗网络架构

当模型都是多层感知机时，对抗性建模框架最容易应用。为了了解生成器在数据 x 上的分布 Pg ，论文定义了输入噪声变量上的先验 Pz(z) ，然后将到数据空间的映射表示为 G(z;eg) ，其中G是由参数 eg 的多层感知器表示的可微函数。论文还定义了输出单个标量的第二个多层感知器 G(z;ed) 。 D(x) 表示 x 来自数据而不是 Pg 的概率。训练D以最大化将正确标签分配给训练示例和来自G的样本的概率。同时训练G以最小化。换句话说，D和G用值函数 V(G,D) 玩两人最大最小博弈游戏：

$\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\\$

公式一要做的是训练一个D，尽可能区分数据来自真实数据还是生成出来的数据，同时训练一个G使得模型尽可能犯错，使得D区分不出来数据是来自真实数据还是生成的数据。在下一节中，将对对抗网进行理论分析，基本上表明，当G和D具有足够的容量时，即在非参数限制下，训练标准允许恢复数据生成分布。请参见图1，以获取对该方法更形象化的解释。在实践中，我们必须使用迭代的数值方法来实现。在训练的内部循环中优化D以完成训练是计算上的禁忌，并且在有限的数据集上会导致过度拟合。相反，我们在优化D的k个步骤和优化G的一个步骤之间交替进行。这会导致D保持在接近其最优解的位置，只要G变化足够慢。算法1正式介绍了该过程。

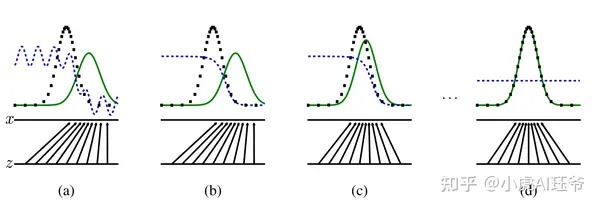
图1：生成对抗网络示例

图1：通过同时更新判别模型分布（D，蓝色，虚线）来训练生成对抗网络，以便区分数据生成分布（黑色，虚线） Px 和生成分布（绿色，实线）的样本。下水平线是 z采样的区域，在这种情况下是均匀的。上面的水平线是 x 域的一部分。向上箭头显示了映射 $x=G(z)$ 如何将非均匀分布 Pg 施加到变换样本上。 G 在 Pg 的高密度区域收缩，在 Pg 的低密度区域扩展。

（a）从z中进行采样映射到绿色高斯分布，D是一个一般的分类器。

（b）训练判别模型D来区分数据来自真实样本还是生成的噪声数据，收敛到 $D^{*}(\boldsymbol{x})=\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\mathrm{data}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}$

（c）更新生成器G，使得鉴别器D很难区分其来自生成的噪声数据 G(z) 。

（d）经过几个步骤的训练，如果G和D有足够的能力，他们将达到一个点，在这一点上，两者都无法改善，因为 $p_{g}=p_{\text {data }}$ 鉴别器无法区分这两种分布，即 $D(x)=\frac{1}{2}$ 在实践中，公式（1）可能无法为G提供足够的梯度，以便更好地学习。在学习的早期，当G值很低时，D可以高置信度地拒绝样本，因为它们与训练数据明显不同。在本例中， $\log (1-D(G(z)))$ 达到饱和。而不是训练G以最小化 $\log (1-D(G(z)))$ ，我们可以训练G使 $\log D(G(\boldsymbol{z}))$ 最大化。这一目标函数在学习早期提供了更强的梯度。

4. 理论结果

生成器G隐式地将概率分布 Pg 定义为 G(z) 当 $z \sim p_{z}$ 因此，如果给定足够的容量和训练时间，我们希望算法1收敛到 Pdata 好的估计值。本节的结果是在非参数设置下完成的，例如，论文通过研究概率密度函数空间中的收敛性来表示具有无限容量的模型。

论文将在第4.1节中说明，对于 Pg=Pdata，这最大最小对策具有全局最优解。然后，将在第4.2节中说明，算法1优化了等式1，从而获得所需的结果。

算法1 生成对抗网的小批量随机梯度下降训练。应用于鉴别器的步数k是一个超参数。在论文的实验中，使用k=1，这是最经济的选项。

for 训练迭代次数 do

　　for k 步骤 do

　　　　. 从噪声先验分布 Pg(z) 中小批量采样m个噪声样本

$\left\{\boldsymbol{z}^{(1)}, \ldots, \boldsymbol{z}^{(m)}\right\}$

　　　　. 从数据真实分布Pdata(x) 中小批量采样m个真实样本

$\left\{\boldsymbol{x}^{(1)}, \ldots, \boldsymbol{x}^{(m)}\right\}$ 。

　　　　. 通过随机梯度上升来更新鉴别器：

$\nabla_{\theta_{d}} \frac{1}{m} \sum_{i=1}^{m}\left[\log D\left(\boldsymbol{x}^{(i)}\right)+\log \left(1-D\left(G\left(\boldsymbol{z}^{(i)}\right)\right)\right)\right]\\$

　　end for

.从噪声先验分布 Pg(z) 中小批量采样m个噪声样本

$\left\{\boldsymbol{z}^{(1)}, \ldots, \boldsymbol{z}^{(m)}\right\}$ 。

.通过随机梯度下降来更新生成器：

$\nabla_{\theta_{g}} \frac{1}{m} \sum_{i=1}^{m} \log \left(1-D\left(G\left(\boldsymbol{z}^{(i)}\right)\right)\right)\\$

end for

基于梯度的更新可以使用任何标准的基于梯度的学习规则。论文在实验中使用了动量。

4.1 Pg = Pdata有全局最优解

论文首先考虑任意给定生成器G的最优鉴别器D。

命题1. 固定G，最佳鉴别器D为：

$D_{G}^{*}(\boldsymbol{x})=\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\\$ 证明：给定任何生成器G，鉴别器D的训练标准是最大化 V(G,D) 。

$\begin{aligned} V(G, D) &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{z} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\ &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x \end{aligned}\\$ 对于任何 $(a, b) \in \mathbb{R}^{2} \backslash\{0,0\}$ ，函数 $y \rightarrow a \log (y)+b \log (1-y)$ 【凸函数,对y求导等于0，即 $a\times\frac{1}{y}-b\times\frac{1}{1-y}=0$ 】 y 取得最大值 a/a+b，取值范围 [0,1] 。

注意，D的训练目标可以解释为最大化估计条件概率 $P(Y=y \mid \boldsymbol{x})$ 的对数似然，其中Y表示x是来自 Pdata （ y=1 ）还是来自 Pg （ y=0 ）。等式1中的最小最大大博弈现在可以重新表述为：

定理1. 当且仅当 Pg = Pdata时，才能达到 C(G) 的全局最小值。此时， C(G) 值为 -log4 。

证明：根据公式（2）对于 $p_{g}=p_{\text {data }}, D_{G}^{*}(\boldsymbol{x})=\frac{1}{2}$ ，所以将 $D_{G}^{*}(\boldsymbol{x})=\frac{1}{2}$ 代入通过公式（4）得到 $C(G)=\log \frac{1}{2}+\log \frac{1}{2}=-\log 4$ 。要确定这是 C(G) 的最佳可能值，当且仅当 Pg = Pdata 时达到，如下：

$\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}}[-\log 2]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}[-\log 2]=-\log 4\\$

用 $C(G)=V\left(D_{G}^{*}, G\right)$ 减去这个表达式【对公式（4）log里面分母配方 1/2 得到KL散度,同时分子乘以 1/2 并从log里面拿出来就变成了 log1/2 】，我们获得：

$\begin{aligned} C(G) &=\max _{D} V(G, D) \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{\frac{p_{\text {data }}(\boldsymbol{x})}{2}}{\frac{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}{2}}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{\frac{p_{g}(\boldsymbol{x})}{2}}{\frac{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}{2}}\right] \\ &=\log (2^{-1})+\log (2^{-1})+K L\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_{g}}{2}\right)+K L\left(p_{g} \| \frac{p_{\text {data }}+p_{g}}{2}\right)\\ &=-\log (4)+K L\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_{g}}{2}\right)+K L\left(p_{g} \| \frac{p_{\text {data }}+p_{g}}{2}\right)\\ \end{aligned}\\$ （5）

其中KL是Kullback–Leibler散度。从而得到真实数据分布和生成模型分布对称的JS散度（JensenShannon divergence）。

$C(G)=-\log (4)+2 \cdot J S D\left(p_{\text {data }} \| p_{g}\right)\\$

由于两个分布之间的Jensen–Shannon散度总是非负的，并且当它们相等时为零，我们已经证明了 $C^{*}=-\log (4)$ 是 C(G) 的全局最小值，当且仅当 Pg = Pdata，即完美复制数据分布的生成模型。

4.2 算法1的收敛性

定理2. 如果G和D有足够的容量，并且在算法1的每个步骤中，允许鉴别器达到其最优解，给定G，并且更新 Pg 进行优化：

$\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right]\\$

最终 Pg 会收敛到 Pdata。

证明.把 $V(G, D)=U\left(p_{g}, D\right)$ 看成一个关于函数 Pg 的函数。其中， Pg 是凸函数，凸函数的上确界函数还是凸函数。凸函数上确界的子导数包括函数在达到最大点处的导数。换句话说，如果 $f(x)=$ $\sup _{\alpha \in \mathcal{A}} f_{\alpha}(x)$ ，并且对于每个 a ， $f_{\alpha}(x)$ 在x中是凸的，那么 $\partial f_{\beta}(x) \in \partial f$ 如果 $\beta=\operatorname{argsup}_{\alpha \in \mathcal{A}} f_{\alpha}(x)$ 。这相当于在给定相应G的情况下，在最优D处进行Pg 的梯度下降更新。 $\sup _{D} U\left(p_{g}, D\right)$ 在 Pg 中是凸的，具有唯一的全局最优解，如定理 1中所证明的，因此在 Pg 更新足够小的情况下， Pg 收敛到 Px ，从而得出结论。

在实践中，我们不通过 Pg 和 e 来优化G的分布，而通过 Pg 和 e 来证明G。然而，多层感知器在实践中的优异性能表明，尽管缺乏理论保证，它们仍然是一个合理的模型。

5.实验

论文训练使用一系列数据集，包括MNIST、多伦多人脸数据库（TFD）和CIFAR-10。生成网络使用纠正线性激活和sigmoid激活的混合，而鉴别器网络使用maxout激活。在训练鉴别器网络时应用了Dropout。虽然论文的理论框架允许在生成器的中间层使用衰减和其他噪声，但论文仅将噪声作为生成器网络最底层的输入。

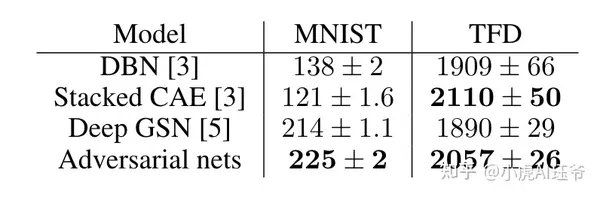
表1：基于Parzen窗的对数似然估计

表1：基于Parzen窗的对数似然估计。MNIST上报告的数字是测试集上样本的平均对数似然，并计算了各示例的平均值的标准误差。在TFD上，论文计算了数据集k折的标准误差，并使用每折的验证集选择了不同的σ。在TFD上，在每折上交叉验证σ，并计算每折上的平均对数似然。对于MNIST，论文将其与数据集的实值（而非二进制）版本的其他模型进行比较。

图2：模型样本的可视化

图2：模型样本的可视化。最右边的一列显示了相邻样本最近的训练示例，以证明模型没有记住训练集。样品是公平的随机抽取，而不是精心挑选的。与其他大多数深层生成模型的可视化不同，这些图像显示的是模型分布中的实际样本，而不是给定隐藏单元样本的条件表示。此外，这些样本是不相关的，因为采样过程不依赖于马尔可夫链混合。a） MNIST b）TFD c）CIFAR-10（全连接模型）d）CIFAR-10（卷积鉴别器和“反卷积”发生器）。

图3：通过在整个模型的z空间中的坐标之间线性插值获得的数字。

论文通过对G生成的样本拟合高斯Parzen窗口，并报告该分布下的对数似然，来估计 Pg 下测试集数据的概率。通过对验证集的交叉验证，得到高斯函数的σ参数。Breuleux等人介绍了这一程序，并将其用于各种生成模型，对于这些模型，精确的可能性是不可处理的。结果见表1。这种估计可能性的方法具有较高的方差，在高维空间中表现不佳，但它是我们所知的最佳方法。生成性模型的发展可以采样但不能估计可能性，这直接推动了对如何评估此类模型的进一步研究。在图2和图3中，论文展示了训练后从生成网络中提取的样本。虽然论文没有声称这些样本优于现有方法生成的样本，但论文认为这些样本至少与文献中更好的生成模型具有竞争力，并突出了对抗性框架的潜力。

6.优缺点

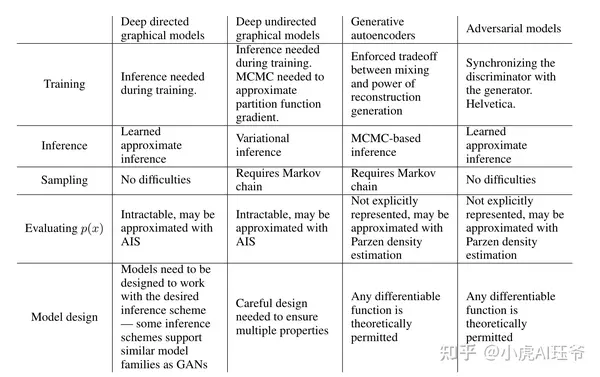
表2：生成性建模中的挑战：对涉及模型的每个主要操作的深入生成性建模的不同方法所遇到的困难进行总结

与以前的建模框架相比，这个新框架有其优点和缺点。缺点主要是 Pg(x) 没有明确的表示，并且在训练期间D必须与G很好地同步（特别是，在不更新D的情况下，G不能训练太多，以避免“Helvetica场景”，在该场景中，G将太多的z值压缩为相同的x值，从而有足够的多样性来建模 Pdata ），就像Boltzmann机器的负链一样，在学习步骤之间必须保持最新。其优点是不需要马尔可夫链，仅使用反向传播获得梯度，在学习过程中不需要推理，并且可以将各种各样的函数合并到模型中。表2总结了生成性对抗网络与其他生成性建模方法的比较。

上述优点主要是计算性的。对抗性模型还可以从生成器网络中获得一些统计优势，该生成器网络不直接使用数据示例进行更新，而仅使用鉴别器的梯度进行更新。这意味着输入的组件不会直接复制到生成器的参数中。对抗性网络的另一个优点是，它们可以表示非常尖锐的，甚至退化的分布，而基于马尔可夫链的方法要求分布有点模糊，以便链能够在模式之间混合。

7.结论和未来的工作

该框架允许许多简单的扩展：

将c作为G和D的输入，可以得到条件生成模型 p(x|c) 。
学习到的近似推理可以通过训练辅助网络来预测给定x的z来执行。这类似于通过唤醒睡眠算法训练的推理网络，但其优点是，可以在生成网络完成训练后，为固定生成网络训练推理网络。
通过训练一系列共享参数的条件模型，可以大致模拟所有条件 $p\left(\boldsymbol{x}_{S} \mid \boldsymbol{x}_{\not S}\right)$ ，其中S是x指数的子集。本质上，可以使用对抗性网络来实现确定性MP-DBM的随机扩展。
半监督学习：当有限的标记数据可用时，来自鉴别器或推理网络的特征可以提高分类器的性能。
效率的提高：通过设计更好的方法来协调G和D，或者在训练期间确定更好的分布来抽样z，可以大大加快训练速度。

论文证明了对抗性建模框架的可行性，表明这些研究方向可能是有用的。