图解大模型训练系列之：DeepSpeed-Megatron MoE并行训练（原理篇）

一、为什么选择DeepSpeed-Megatron

引入MoE并行训练的框架有很多，为什么这篇文章选择用DeepSpeed来做讲解呢？主要原因如下：

• 使用DeepSpeed做讲解时，可将其MoE实现作为主线，其余框架MoE实现作为分支，这样方便在讲解主线的同时，引入分支进行对比。之所以DeepSpeed能成为主线，是因为它的MoE代码是一个“大杂汇”，例如，它的MoE初始化设置借鉴了Megatron，它的MoE-Layer架构借鉴了Fairscale，它的MoE优化方式借鉴了Tutel等，在这些借鉴之上，它引入了自己的一些改进。所以使用DeepSpeed，更方便我们做对比讲解。

• DeepSpeed的MoE模型架构是Gshard。作为最早将MoE应用在Transformer上的模型，Gshard提出的框架和思想一直影响至今。后续我们看到的很多LLM MoE的架构改进，其实都是在Gshard的这一套逻辑上做的迭代，比如loss改造、topKexpert的选择，稀疏矩阵计算优化等等。所以从Gshard入手，更利于我们对基础的把握。

二、Gshard架构

2.1 直觉上理解MoE设计

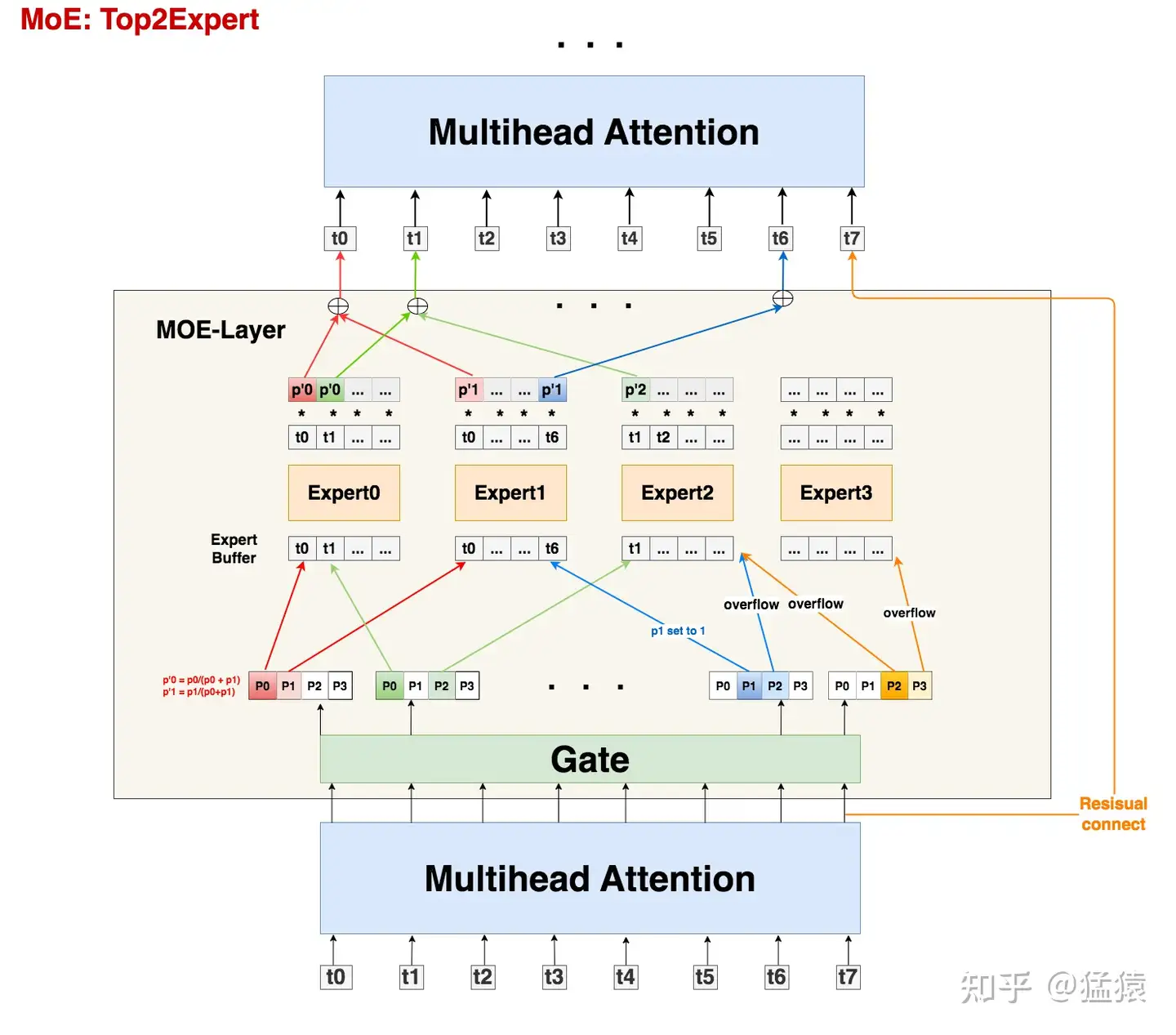
从架构图中我们可以发现，MoE其实就是将Transformer中的FFN层替换成了MoE-layer，其中每个MoE-Layer由一个gate和若干个experts组成。这里gate和每个expert都可以理解成是nn.linear形式的神经网络。


这样设计的直觉是什么呢？

• expert：术业有专攻。假设我的输入数据是“我爱吃炸鸡”，在原始的Transformer中，我们把这5个token送去一个FFN层做处理。但是现在我们发现这句话从结构上可以拆成“主语-我”，“谓语-爱吃”，“宾语-炸鸡”，秉持着术业有专攻的原则，我把原来的1个FFN拆分成若干个expert，分别用来单独解析“主语”，“谓语”，“宾语”，这样可能会达到更好的效果。

• gate：那么我怎么知道要把哪个token送去哪个expert呢？很简单，我再训练一个gate神经网络，让它帮我判断就好了。

当然，这里并不是说expert就是用来解析主谓宾，只是举一个例子说明：不同token代表的含义不一样，因此我们可以用不同expert来对它们做解析。除了训练上也许能达到更好的效果外，MoE还能帮助我们在扩大模型规模的同时保证计算量是非线性增加的（因为每个token只用过topK个expert，不用过全量expert），这也是我们说MoE-layer是稀疏层的原因。


最后需要注意的是，在之前的表述中，我们说expert是从FFN层转变而来的，这很容易让人错理解成expert就是对FFN的平均切分，实际上你可以任意指定每个expert的大小，每个expert甚至可以>=原来单个FFN层，这并不会改变MoE的核心思想：token只发去部分expert时的计算量会小于它发去所有expert的计算量。


接下来，我们来看上图中MoE的各部分细节，下文中所有的符号遵从Gshard论文表示。

2.2 输入数据

首先，所有tokens正常过Attention层得到MoE-layer的输入，我们记输入数据的尺寸为(S, M)，其中:

• S : 输入batch中的token数量，例如图中S=8

• M: token_embedding维度

需要注意的是，我们一般是以batch的形式组织输入数据的（图中batch_size = 1），假设Attention层输入数据的维度是(batch_size, seq_len, M)，那么有S = batch_size * seq_len

2.3 Gate

接下来，我们就要使用线形层Gate帮助我们判断token应该送去哪个expert了。在别的MoE架构中，Gate有时也被称为Router（路由）。Gate的尺寸大小为(M, E)，其中E表示expert的数量。


输入数据(S, M)过Gate(M, E)后，得到prob数据(S, E)，它的含义是：每个token去向每个expert的概率。
由于在Gshard中我们使用的是top2Expert，因此对每个token，我们只关心它概率最大的两个expert。在图中，我们用深色表示最大概率，浅色表示次大概率。例如对token0来说，它被送去expert0的概率最大，被送去expert1的概率次大。


好，现在既然知道每个token的top2Expert了，是不是就可以直接发送了呢？别急，我们先来看看Expert的架构

2.4 Expert与溢出处理

我们知道，token发去expert的概率不是我们能控制的，在实际操作中，可能某些expert接收到了好多token，而某些expert接收的token寥寥无几，我们管这种现象叫expert负载不均。这种情况不仅不符合我们MoE的设计初衷（术业有专攻），还影响计算效率（例如引起分布式训练中各卡通讯时的负载不均），所以我们急需想办法缓解这种问题，Gshard就提出了以下几种解决办法：


（1） capacity和capacity factor

在图中，你会看到一个叫Expert buffer的东西，这是什么呢？


在上文中我们提到，有些expert可能接收到非常多的token，为了缓解这个问题，我们可以给每个expert设置一个容量值（capacity），如果当前这个expert接收到的token数已经超过了容量，那么它就不再接收token了，此时我们称这个多出来的token为溢出(overflow)。


那么容量应该怎么设置呢？在我们的例子中，一共有8个token和4个expert，在理想的负载均衡的情况下，每个expert应该接收8/4 = 2个token，考虑到这里采用的是top2Expert，因此最终每个expert接收的token上限最好是(8/4)*2 = 4，这也是我们图中expert buffer的长度。


但这并不说明capacity一定要是 𝑆𝐸∗𝐾 。我们可以在此基础上使用capacity factor，根据需要让每个expert多处理或少处理一些token；你甚至还能设置一个容量下界(min_capacity)，所以最终capacity可以按如下式子定义：

𝑐𝑎𝑝𝑎𝑐𝑖𝑡𝑦=𝑚𝑎𝑥(𝑆𝐸∗𝐾∗𝑐𝑎𝑝𝑎𝑐𝑖𝑡𝑦_𝑓𝑎𝑐𝑡𝑜𝑟,𝑚𝑖𝑛_𝑐𝑎𝑝𝑎𝑐𝑖𝑡𝑦)


回到图中的例子上来，我们发现t0和t1都正常发去top2Expert上了。但是对于t6，它的2nd expert已经装满了；对于t7，它的1st和2nd expert都满了。所以t6和t7都发生了溢出。那么我们要怎么处理溢出的情况？别着急，我们马上来看。


（2） Random Routing

对于一个token，我们一定要把它发到top2Expert上吗？
从直觉上对于每个token，我们最好将其以100%的概率发去1st expert；但是对于它的2nd expert，我们可以不100%发送，而是以一定的概率（例如从uniform(0,1)中随机抽取一个数p，将其作为概率）发送，这样不就能节省对expert capacity的消耗，从而更好利用每个expert吗？这也是Gshard论文中提出的方法。


而我们下文要讲的DeepSpeed代码，在这一块又做了稍微不同的处理：以图中t0为例，1st expert它是肯定要发去的。但是在选择2nd expert时，它做了一些加噪处理：对产出的每个概率（更确切地说是logit），它从某种分布中采样4个噪声，加在这4个logit上，然后mask掉1st expert位置的logit，再从剩下3个logit中找到最大的作为其2nd Expert。


现在我们已经选出最终的top2Expert，我们再回到没有加噪时的4个概率上，取出相应位置的概率，做normalize计算：
𝑃0′=𝑃0𝑃0+𝑃1,𝑃1′=𝑃1𝑃0+𝑃1


$ 𝑃0′,𝑃1′ 是一种权重（weight），该token过expert0和expert1后会分别得到一个输出token，我们可以对2个输出token做加权计算，得到最终的输出token。


回到上面的问题，token发生溢出时，要怎么办呢？

• 如果只有单个expert溢出，那么就把另一个expert的权重值为1，然后正常参与加权计算（如图中t6）

• 如果2个expert都溢出，那么该token就不经过任何expert，直接通过残差连接的方式，原样发去下一层的Attention上（如图中t7）

（3） Auxiliary Loss

除了capacity和random routing外，Gshard还通过增加一项辅助损失函数(Auxiliary Loss)来尽量保证Expert的负载均衡，其定义如下：
𝑙𝑎𝑢𝑥=1𝐸∑𝑒=1𝐸𝑐𝑒𝑆∗𝑚𝑒

其中：

• 𝐸 ：专家数量

• 𝑐𝑒 ：某个专家的buffer中已经存下的token数量（一般指该专家作为1st专家时接收到的token数）

• 𝑆 ：总token数量

• 𝑚𝑒 ：某个专家的buffer中已经存下的token在该专家上的avg(weight)（token考虑范围也是那些将该专家作为1st专家的token）

我们将这个辅助损失添加在正常loss之后，我们的目标也是最小化这个辅助损失。这个辅助损失设计已经非常直觉，就不过多阐述了。值得一提的是，之所以引入 𝑚𝑒 项，是为了让辅助损失函数可以bwd求导（因为只考虑 𝑐𝑒𝑆 这项，它受制于argmax，是不可求导的，实在难理解也没关系，记住就好）。

2.5 Zero Padding和Drop tokens

写到这里，我们稍微总结下：

• 首先，我们有一串过Attention层后的token序列

• 我们通过Gate，计算每个token去往每个expert的概率

• 我们希望不同expert处理的token数尽量均衡，所以我们同时采取三方面优化：
  

  • Capacity: 为每个expert设置capacity（expert buffer），限制它能处理的最大token数量，多出来的token算为溢出，在top2Expert都溢出的情况下，该token会被直接发去下一层attention。

  • Random Routing: 每个token一定会被发去1st Expert，在此基础上我们通过random routing加噪的方式，重新选出2nd expert。在做完capacity + random routing后，我们最终确认了每个token要发去的top2expert和其对应的权重，通过加权计算的方式，确认Moe-Layer最终的输出结果。

  • Auxiliary Loss：添加辅助损失函数，对expert负载不均的情况做进一步惩罚。

到这里，Gshard MoE的核心架构内容我们就说完了，最后再提2点：


（1）Zero padding

我们上述的优化方法，只能“缓解”负载不均，而不能保证解决负载不均。也就是说，存在一些Expert，它的Expert buffer没有填满，这可怎么办呢？


最直接的方法，就是在没有buffer中空出来的位置，用0向量填充，我们称为Zero padding。更具体地说，最终每个expert上的输入数据维度为(E, C, M)，其中C表示capacity。0填充的好处是，我们保证每个expert上要处理的输入数据维度是一样的，这有利于硬件层面的后续处理（例如多卡通讯间的负载均衡等）。

（2）Drop tokens
我们知道，当发生溢出情况时，不是所有token都会被expert正常处理的，我们称这种对溢出的操作为drop tokens。如果被drop掉的tokens数量太多，也是一种信息损失（它们都没经过任何expert解析），我们当然可以通过调整capacity来缓解这个问题，但过大的capacity会引起更严重的zero padding问题（影响到矩阵的稀疏程度），所以这也是后续一些MoE模型架构侧重的优化。

2.6 伪代码

现在我们将整个过程以伪代码的形式写出（大家注意看注释细节）。这里在Gshard论文提供的伪代码上，按照deepspeed的实现方式做了些修正。

# -------------------------------------------------------------------------------------
# 1.通过gate，计算每个token去到每个expert的概率
# 
# 【input】：Attention层输出的一整个batch的token，其尺寸为(seq_len, batch_size, M),
#             其中M表示token_embedding
# 【reshaped_input】：由input做reshape而来，尺寸为(S, M), 其中S = seq_len * batch_size
# 【Wg】: gate的权重，尺寸为(M, E)，其中E表示MoE-layer层的专家总数
# 【gates】: 每个token去到每个expert的概率，尺寸为(S, E)
# -------------------------------------------------------------------------------------
M = input.shape[-1]
reshape_input = input.reshape(-1, M)

gates = softmax(enisum("SM, ME -> SE"), reshape_input, Wg)

# -------------------------------------------------------------------------------------
# 2. 确定每个token最终要去的top2Expert，并返回对应的weight和mask
#
# 【combine_weights】：尺寸为(S, E, C)，其中C表示capacity（Expert buffer）。
#                     表示对每个token（S）而言，它对每个专家（E）的weight，而这个weight按照
#                     该token在buffer中的位置（C）存放，不是目标位置的地方则用0填充
#                     例如图中token1，它将被发送到expert0和expert2，且它在expert0的buffer中排在
#                     1号位置，在expert2中排在0号位置，那么token1的combine_weights就是：
#                     [[0., p0, 0., 0.],
#                     [0. , 0.,  0., 0.],
#                     [p2, 0.,  0., 0.],
#                     [0.,  0.,  0., 0.]]
#                     最后再复习一下weight和gates所表示的prob的区别：前者是在后者基础上，
#                     做了random + normalize，确定最终的top2Expert后返回的对应结果
# 
# 【dispatch_mask】：  尺寸为（S，E，C），它等于combine_weights.bool(), 也就是对combine_weights
#                     为0的地方设为False，为1的地方设为True。
#                     dispatch_mask后续将被用在zero padding上
# -------------------------------------------------------------------------------------
# (S, E, C)      (S, E, C)
combine_weights, dispatch_mask = Top2Gating(gates)


# -------------------------------------------------------------------------------------
# 3. 将输入数据按照expert的顺序排好，为下一步送去expert计算做准备（很重要）
# 
# 【dispatch_mask】：尺寸为（S, E, C），定义参见2
# 【reshape_input】：尺寸为(S, M)，定义参见1
# 【dispatched_expert_input】：本步的输出结果，表示按专家排序好的输入数据，尺寸为(E, C, M)
#  这个结果表示，每个专家（E）的buffer（C）下要处理的token_embedding（M），
#  例如dispatched_expert_input[0]就表示expert0 buffer中的情况
#  注意：
#  （1）每个专家buffer中的token是按顺序排列好的，
#       回到图中的例子，expert0 buffer下0号位置排的是token0，
#       3号位置排的是token6，以此类推。dispatch_mask就起到了维护这种顺序的作用
#  （2）当对应专家接收的token数不足buffer长度C时，不足的地方用0向量填充。
# -------------------------------------------------------------------------------------
dispatched_expert_input = einsum("SEC, SM -> ECM", dispatched_mask, reshape_input)

# -------------------------------------------------------------------------------------
# 4. 将排序好的input送入expert进行计算。
#    同正常的FFN层一样，每个expert也由2个线形层Wi, Wo组成
# 【dispatched_expert_input】：按专家顺序和专家buffer中的token顺序排好的输入数据，
#                             尺寸为(E, C, M)，具体定义见3
# 【Wi】：experts的Wi层，尺寸为(E，M, H)，
# 【Wo】：experts的Wo层，尺寸为(E, H, M)
# 【expert_outputs】：experts的输出结果，不含加权处理，尺寸为（E, C, M）
# -------------------------------------------------------------------------------------
h = enisum("ECM, EMH -> ECH", dispatched_expert_input, Wi)
h = relu(h)
expert_outputs = enisum("ECH, EHM -> ECM", h, Wo)

# -------------------------------------------------------------------------------------
# 5. 最后，进行加权计算，得到最终MoE-layer层的输出
# -------------------------------------------------------------------------------------
outputs = enisum("SEC, ECM -> SM", combine_weights, expert_outputs)
outputs_reshape = outputs.reshape(input.shape) # 从(S, M)变成(seq_len, batch_size, M)

再特别说明几点

（1）enisum的作用

• enisum在这里泛指我们自定义的某几种矩阵计算方式，enisum中诸如"SEC, SM -> ECM"只是用来表示输入数据和输出数据的维度，并不表示两个输入矩阵就一定是按照SEC和SM这样的尺寸直接相乘（我们肯定要对输入数据做些例如unsqeeze()，reshape()之类的操作才能把它们正确乘起来，得到想要的结果）。

• enisum使得我们在矩阵计算的同时，能维持token和expert的顺序。你可能在阅读伪代码的过程中已经感受到，维持“顺序”是一件很重要的事，例如token在专家buffer中的顺序，各个专家间的排序等。为什么维持顺序很重要呢？因为一个batch里有很多token，我们将其发往不同的expert做计算后，输出结果的顺序肯定是打乱的，所以需要通过一种方式追踪顺序，把token permute回正常的位置再输入下一层Attention。在这里我们通过自定义的矩阵计算方式，巧妙维护住这种顺序，这样我们就不需要额外建索引表之类的来查找了。

在后文对deepspeed的源码解读中，我们会看到enisum的具体定义。不过这块不是源码解读的讲述重点（毕竟也只是矩阵计算而已）。对这块有兴趣的朋友，可以自己攥一些数据跑跑代码，研究它的运作原理。不感兴趣的朋友，只要记住输入输出的尺寸及各自含义即可。


（2）将输入数据按照expert的顺序排好
大家可以特别关注下伪代码步骤3中的操作，这个操作将有利于后续专家并行组之间的通讯。

三、MoE并行训练

正如前文所说，阅读本章需要了解Megatron混合并行原理，并掌握其代码中“分布式初始化”部分的相关知识。


当我刚开始研究MoE时，总会看到类似EP + DP，EP + TP + DP这样并行方式的缩写，例如DeepSpeed官方文档中所描述的。最开始我对这个符号的理解是：非MoE层的部分采取DP或DP+TP的方式；而MoE层的部分采取一种叫EP的新方式。然而当我把这样的理解代入代码中时，却发现有些部分难以解释。


摸索了一段时间后，我才发现不管是EP + DP，EP + TP +DP等等，它们都在特指MoE层的并行方式；而对non-MoE层，你采取什么样的并行方式，是不在这些并行符号的表示范围中的。


我们以EP + DP，EP + TP + DP这两种方式为例，来看看如何对MoE模型做分布式初始化。

3.1 EP + DP

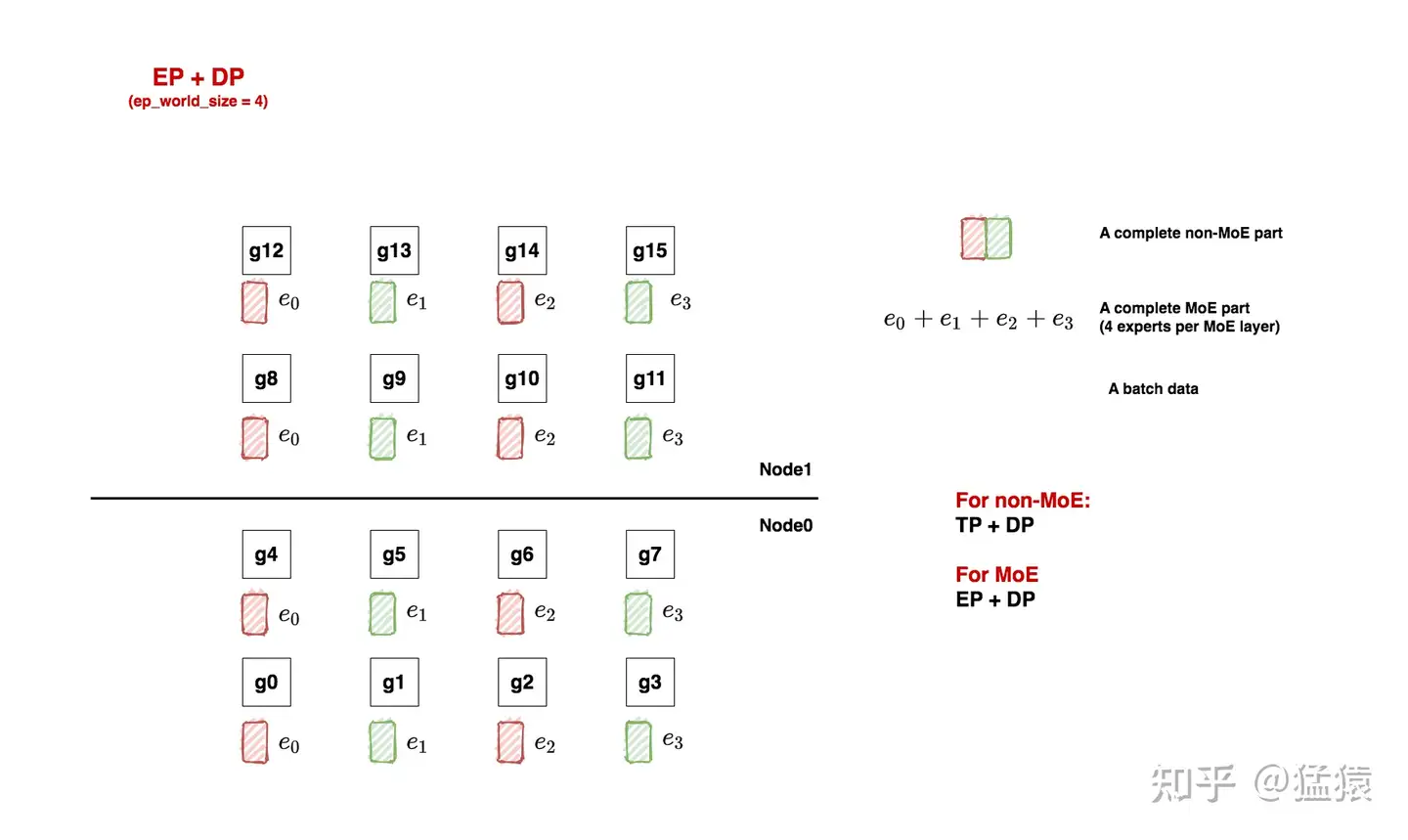
如上图，我们先来看一个例子。在本例中，我们共有16块gpu：

• 对于non-moe的部分，采取tp + dp并行

• 对于moe部分，采取ep + dp并行。

（1）Non-MoE: tp + dp

non-moe的部分指模型中Attention、word embedding层等。tp + pp 的并行方式我们也很熟悉了，根据图中所示，我们有：

tp_world_size = 2
tp_groups = [
             [g0,  g1],[g2, g3], [g4, g5], [g6, g7],
             [g8,  g9],[g10, g11],[g12, g13],[g14, g15]
            ]

dp_world_size = 8
dp_groups = [
              [g0, g2, g4, g6, g8, g10, g12, g14],
              [g1, g3, g5, g7, g9, g11, g13, g15]
            ]

pp_world_size = 1

（2）MoE: ep + dp

当我们安顿好non-moe的部分后，我们就可以开始考虑要怎么安排MoE层了，这里我们先给出划分方法，然后再对其进行详细解释：

ep_world_size = 4
ep_groups = [
             [g0,    g1,    g2,     g3 ],
             [g4,    g5,    g6,     g7],
             [g8,    g9,    g10,  g11],
             [g12,  g13,  g14,  g15]
            ]

ep_dp_world_size = 4
ep_dp_groups = [
                 [g0,   g4,   g8,   g12],
                 [g1,   g5,   g9,   g13],
                 [g2,   g6,   g10, g14],
                 [g3,   g7,   g11, g15]
                 ]

ep_tp_world_size = 1

还记得前面我们说MoE层采用的是EP + DP并行吗？那么这里的EP和DP的定义到底是什么呢？


假设我们每个MoE层有若干个专家（我们统称其为一套专家），现在我们想把这一套专家分布排列到gpu上，最直觉的做法就是：我们先定好要用几块GPU装下一套专家（EP），进而我们就能确认全局上共有多少套专家副本在跑（DP）。通过这种简单的方式，我们就做好了EP + DP形式的MoE层初始化。


回到我们的例子中，一共16块GPU：

• ep_world_size = 4：表示我们希望用4块GPU装下一套完整的专家。确定这个数值后，我们就能确认ep_groups

• local_expert_num：expert_num / ep_world_size，其中expert_num表示每层专家的总数。假设每层专家数量是4，那么1块gpu上就放一个专家；假设每层专家数量是8，那么1块gpu上就放2个专家。所以图中的e0等符号并不绝对表示这里只有1个专家，只是对local_expert的统称。

• ep_dp_world_size：类比于non-MoE层，MoE层同样也有数据并行的概念。例如图中[g0, g4, g8, g12]上都维护着e0，所以它们构成一个ep_dp_group。这个group的作用是当我们在计算bwd时，它们之间是需要做梯度的allreduce通讯的，我们会在下文详细图解这一点。另外需要注意的是，构成ep_dp_group的条件不仅是e相同，还需要每个e吃的batch的数据不同（类比于一个普通的dp_group，组内的每张卡吃的是不同的小batch）。现在你可能无法具象化感受这点，我们在后文将ep+tp+dp并行的时候再细说。

• ep_tp_world_size：类比于non-MoE层，MoE层同样也有张量并行的概念，即一个专家可以纵向切割成若干份，本例中我们不对专家做tp操作，在后文我们会详细来看做了tp操作的相关例子。

额外再说明两点：

• 你可能发现上面诸如ep_dp_world_size这样的符号有点陌生，因为你并没有在相关论文/代码中看到过它。这是因为不同框架对MoE并行的相关概念定义鱼龙混杂，除了符号不一外，有时相同的符号甚至表示不同的含义，这也是最令我痛苦的点。所以这里我自定义了一套符号，不管是什么框架，我都会把它的定义映射到这套符号上来。

• 以图中的e0来举例，我们再强调两点：首先，如上文所说，它不绝对表示1个专家，只是对local_expert的统称。其次，它不绝对表示1个MoE层的专家，它表示所有MoE层放在这块卡上的专家统称。

相信现在你对EP+DP的分布式设置有了初步认识了（这里我们特意举了non-MoE是tp+dp，而不是单纯dp的例子，来说明ep+dp这个并行定义是专门针对MoE部分的），但你可能对那些并行group的作用还不能有具象体会。现在让我们来给模型喂点数据，看看在1个FWD和BWD过程中，这些group都做了什么通讯吧！


（3）FWD与BWD过程

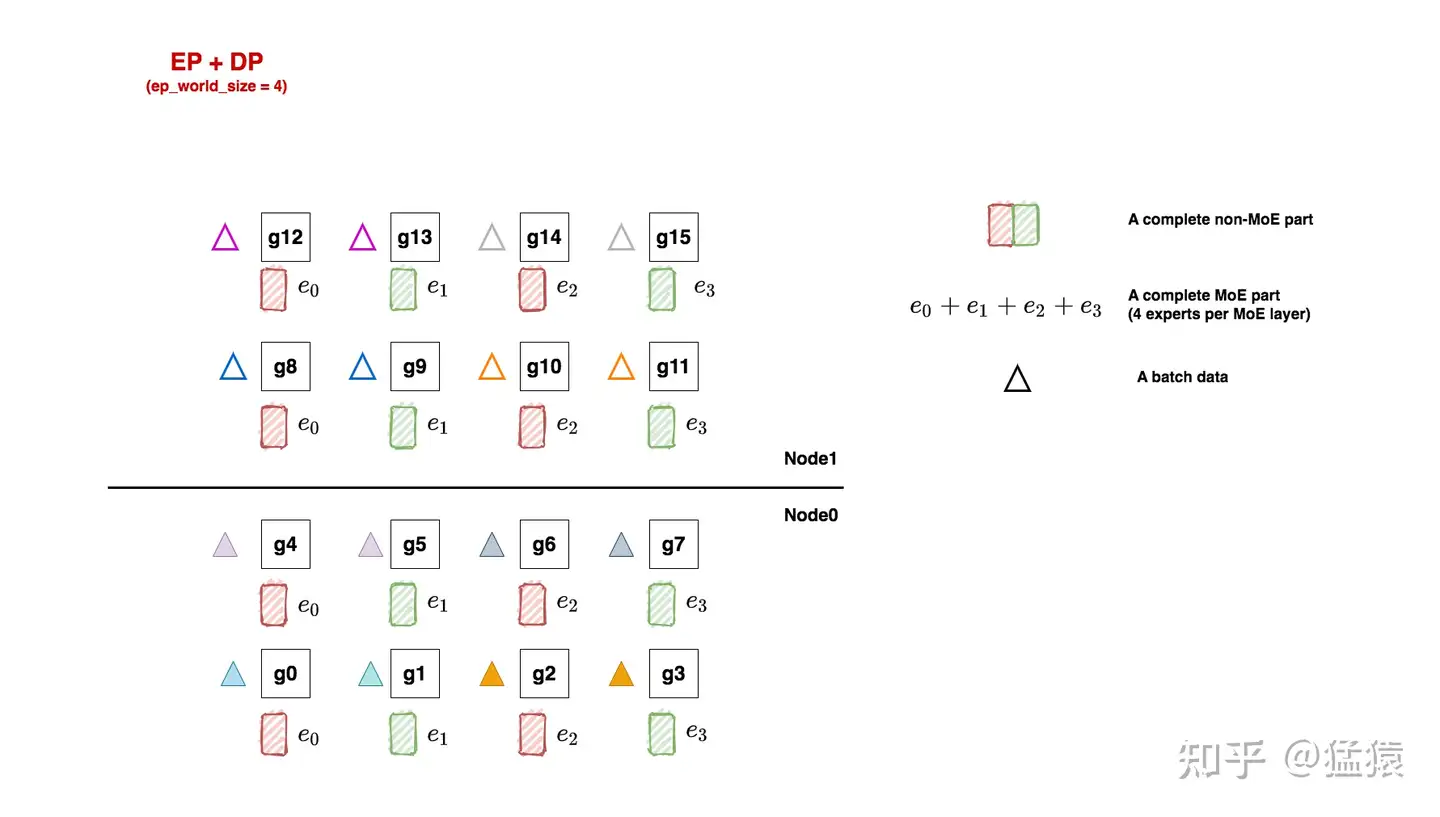
如图，三角形表示1个batch的数据，这里我们共喂给模型8个batch。每个tp组内的输入数据一致，所以它们对应的三角形颜色也相同。


好，让我们牢记分布式并行的使命：分布式训练效果应与单卡（假设这个单卡能装下一个完整的模型）的训练效果一致。放到我们的例子里，16卡吃8个小batch做完FWD+BWD后的结果，应该与单卡吃下由这8个小batch组成的大batch的结果一致。


现在开始做FWD与BWD，过程如下图：

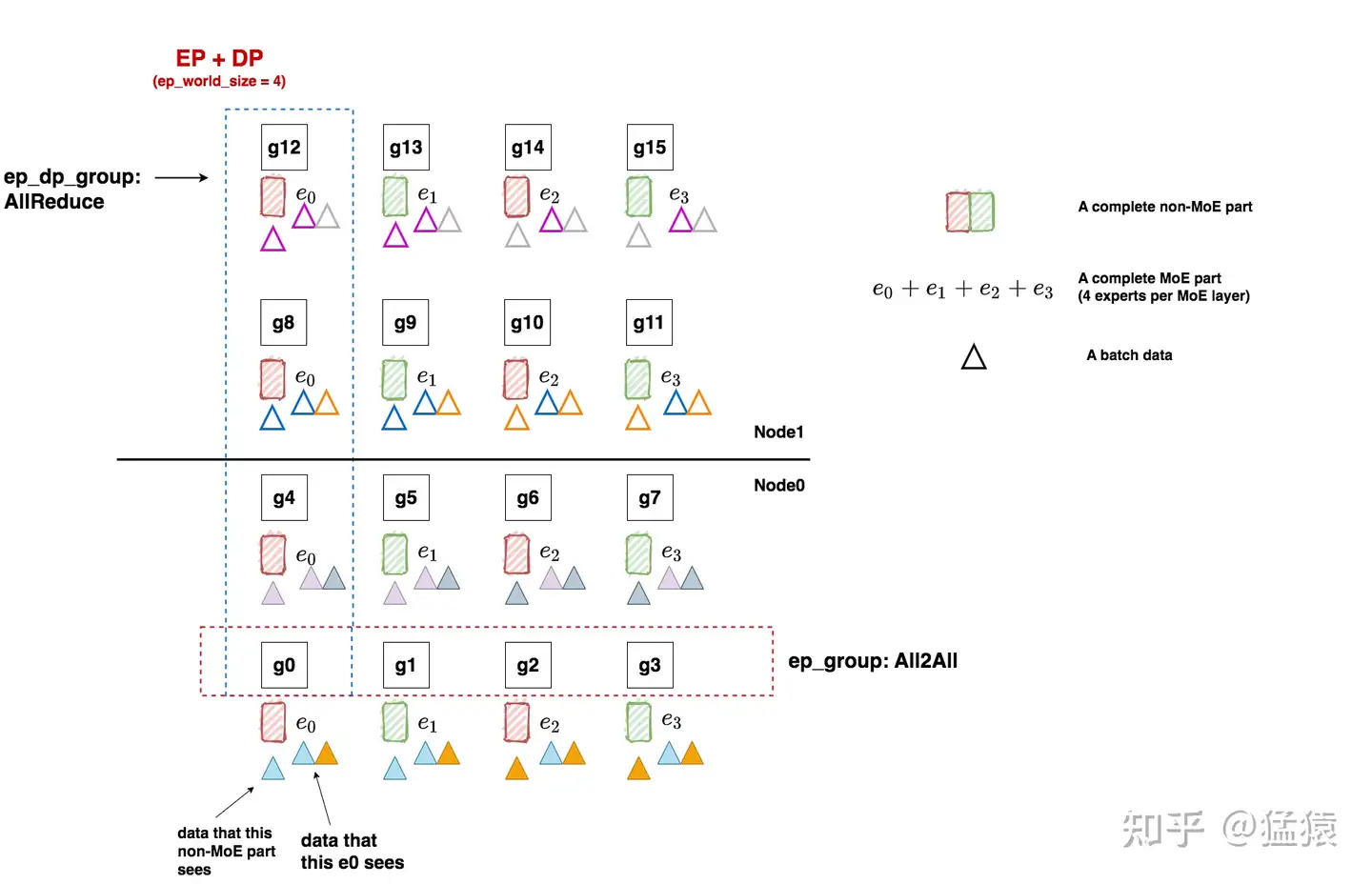
• 在FWD中，数据先过non-MoE（Attention）层，由于一个tp组内每块卡的输出也是一致的，因此三角形颜色的分布没有改变。我们把三角形移动到对应的non-MoE分块下，表示在整个FWD中对应的non-MoE分块见过的batch。

• 继续做FWD，现在数据来到了MoE层，我们前面说过，每块卡上数据的维度是(E, C, M)，即我们已经计算好token和专家的对应关系，我们只需在ep_group内做all2all通讯，将token发送去对应的专家即可，这就是ep_group的作用。all2all通讯的细节我们放在后面说，这里只需记住在all2all通讯后，ep_group内每个专家见过的batch有了改变，例如对e0，现在它见过了蓝色和橘色两个batch的数据。每个专家计算完自己的结果后，再通过all2all的方式，将对应的token计算结果还给ep_group内的各gpu，然后继续mon-MoE->MoE的步骤，知道FWD完毕。

• 做完了FWD，进入BWD。我们首先来到MoE部分，以e0为例，根据分布式训练使命，我们应该allreduce 8个batch的梯度结果，用来更新e0。欸那这8个batch在哪里呢？当然是在图中的ep_dp_group内！所以在BWD过程中，我们对ep_dp_group中e0的梯度做allreduce，用来更新e0。现在，你是不是更好理解ep_group的作用了！

• 继续做BWD，数据来到了non-MoE部分，这块对梯度的通讯我们在Megatron解析中已经讲了很多，这里就不再说明了。

总结一下针对MoE部分的重点：

• 在FWD中，ep_group进行all2all通讯，将token发去对应的专家做计算，并将计算结果取回。

• 在BWD中，ep_dp_group进行AllReduce通讯梯度，用于更新对应的专家的参数。

对于这种在non-MoE部分采用tp，在MoE部分不采用tp的设计，在代码实现上有几个点要注意。举例来说，对non-MoE来说，[g0, g1]是一个tp组，我们要对这两块卡的输出做AllReduce。但是对MoE部分而言，[g0, g1]的输出是不需要做AllReduce的。看过Megatron代码的朋友，应该能想起这块相关的操作在RowParallelLinear/ColumnParallelLinear模块下，所以在deepspeed中，通过传入一个enable_expert_tensor_parallelism=True/False的参数来做相关调整，这点我们放在源码解读篇中说。

在一些代码框架（例如Megatron）中，为了多复用已有的并行方式，少做修改，一般都会做些强硬限制：例如MoE的mp（tp与pp）层面的并行设置须与non-MoE的mp设置保持一致，即如果non-MoE做了tp切分，MoE也必须以同样的方式做tp切分，在此基础上再去安排MoE的ep/ep_data等等并行。在这样的限制下，如果non-MoE采用dp，那么MoE只能用ep+dp；如果non-MoE采用tp+dp，那么MoE只能采用ep+tp+dp；欸发现了没有！这是不是和你我对ep+tp+dp这个符号表示的初印象很像？即tp+dp是non-MoE的并行方式，ep是MoE的并行方式。所以这样的理解，在某些代码框架上是通的，但是到别的更为灵活的代码实现上，就产生矛盾了。这也为什么我在本章开头说明，最好统一把这个符号理解成是对MoE部分并行方式的描述。


对于non-MoE只采用dp，MoE采用ep+dp的设计，比较简单，这里我们就不多说了，大家可以自己画画。

3.2 All2All通讯

在3.1中，我们说过每张卡进MoE前的输入数据尺寸为(E, C, M)，其中E表示expert_num，C表示capacity，M表示token_embedding。在每个ep_group内，我们通过all2all通讯将token发去指定的expert做计算，再通过all2all通讯将计算结果返回。现在我们来介绍all2all的细节。


（1）基础All2All

我们先来看基础All2All是怎么做的，再来看deepspeed改进后的All2All是怎么做的。

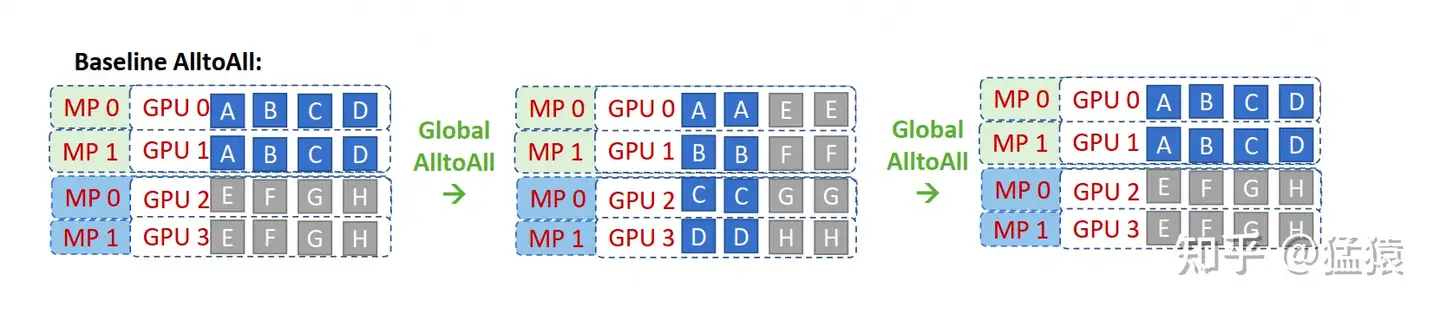
图中的MP表示的就是TP（在deepspeed的语系中，MP=TP），图中相关的分布式group为：

• tp_group: [[g0, g1], [g2,g3]]

• ep_group: [[g0,g1,g2,g3]]，也就意味四张卡上分别存着e0, e1, e2, e3

我们先来看最左侧的图，它描绘了数据刚过完non-MoE(Attention)层后的结果。因为tp组间做了AllReduce，所以g0和g1上存的数据完全一致（ABCD），g2和g3上存的数据完全一致(EFGH)。我们以[g0,g1]为例，因为有4个专家，所以图中将数据分为ABCD四份，每一份的维度为(C, M)，四份总维度为(E, C, M)。也就是说A的数据要发去e0，B的数据要发去e1，以此类推。

我们再来看中间的图，它描绘了ep_group内首次做all2all的过程，这个过程的目的是将token发去对应的expert上进行计算。你是否已经发现，all2all就相当于做了一次矩阵转置（对比一下左侧图和中间图的数据块排布）？因此通过All2All，我们就让数据块去到了它对应的位置：AE去e0，BF去e1，以此类推。而为了实现这种转置，我们必须提前对non-MoE做分块排序，让它按照要去的专家位置排好，现在你是不是能感受到排序的意义了？

最后来看右侧的图，它描绘了ep_group内第二次做all2all的过程，这个过程的目的是将MoE算完的token再返回给各卡，原理和上述一致。

一切都进行地很顺利，但我们能不能再做些优化呢？例如，属于一个tp组的g0和g1上存着一模一样的数据，在all2all的过程中是会被重复发送和计算的，我们能不能减少这种重复？

（2）改进All2All，理论版

为了避免tp组内的数据重复发送的问题，deepspeed在论文中提出了一种改进版的All2All算法，但值得一提的是，deepspeed在代码实现中可不是完全按照这种改进算法来的（手动狗头，虽然实现上还是借鉴了一些理论上的思路）。所以本节我们先来看deepspeed在理论上的改进，然后再来看它的实操。

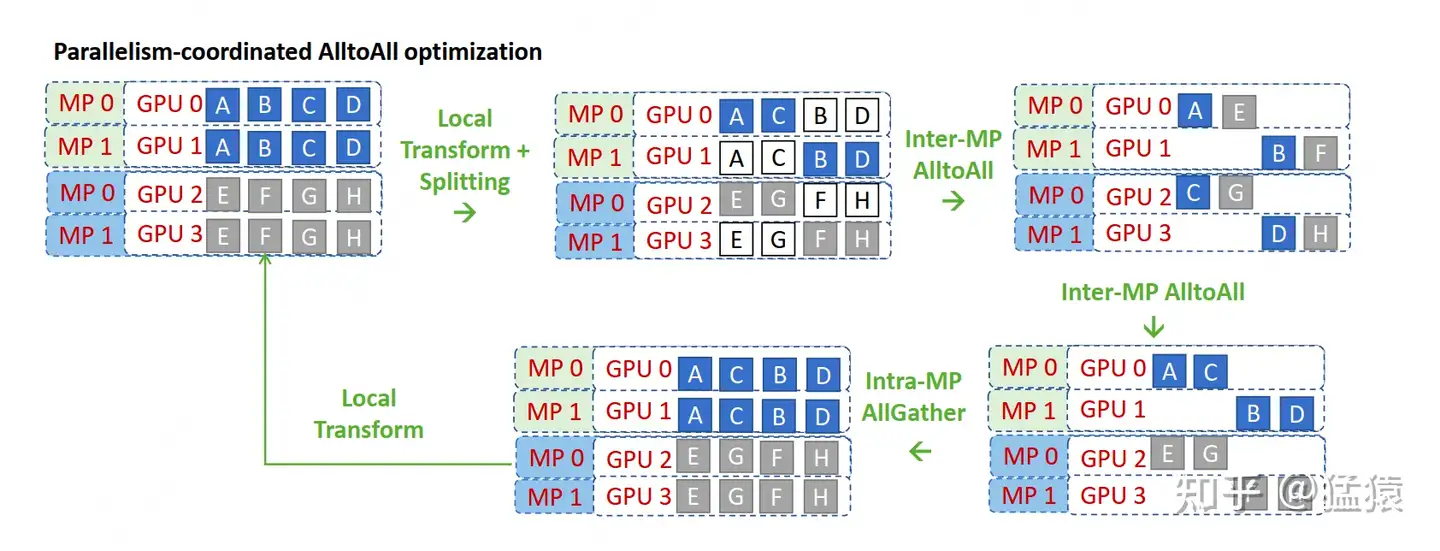
咱们来看看这张图，确实是维持了deepspeed团队一贯的禅意风格：以培养读者悟性为宗旨，能不点破就不点破。所以我们也不要辜负他们的期望，努力地悟一悟吧！


deepspeed改进版all2all的核心宗旨是：既然你说tp组间的数据重复，那么我就在tp组间砍一刀，让tp组内的每块卡都维护不同的数据，不就不行了么？于是我把g0上的CD砍掉，g1上的AB砍掉，以此类推。这下完美了吧，每块卡上只有2块数据且不重复了！
但这样一来，all2all要怎么做呢？你现在每张卡上只有2个数据块，但是all2all group内一共4块卡，如果你想正常做all2all，必须卡上的数据块和卡数相同才行，否则就会出现问题。


所以，我们再想另一个办法：如果现在卡上只有两块数据了，那我如果把all2all group也一分为二，每个group内2张卡，一共两个all2all group，不就能解决这个问题了吗？那这个新的all2all group要怎么设呢？最简单的方法就是，tp rank相同的卡组成一个新的all2all group。例如对g0和g2，它们的tp_rank都是0，所以它们组成新的all2all组，g1和g3也是同理。所以现在，我们只需对[g0, g2] all2all，[g1, g3] all2all就可以了。这也是为什么在图中把CB和FG交换位置的原因。
那如果我想[g0,g3]all2all，[g1,g2]all2all，然后把CD, GH交换位置，那可以么？理论上是没问题的，但是代码上这样写就不太优雅了，比不上同一个tp rank间all2all来得简便。


知道了这个流程，我们再来看上面的图，是不是一目了然了？图中local transform为改进版all2all作准备，交换了数据；两个all2all就是token发送和接受的过程；最后再加一个all-gather，因为tp组内每块卡的输出要保持一致，这样才能进入接下来的non-MoE层继续计算。


（3）改进All2All，实操版

好，理论我们已经知道了。但你从改进的过程中肯定也发现了：原来是4卡all2all，现在是2卡all2all，这不就把我辛苦设置好的ep_group破坏掉了吗？如果真的这么操作，那对代码的改动肯定是比较大的。


所以，有没有办法还是4卡all2all，但是也避免发送重复数据呢？


当然有，大家想想我们每张卡的输出数据维度(E, C, M)，同个tp组内的所有卡这个(E, C, M)是一致的，此时你的脑子是不是灵光一现：如果我沿着C把数据切成tp_world_size份，每张卡只保留其中的一份，那么不就既能做到tp组内卡上的数据不重复的情况下复用原来的ep_group做all2all吗？在两次all2all后，我依然通过一个all-gather操作还原tp组内的完整数据，这不就行了吗？这就是deepspeed在代码实操中使用的方法。


deepspeed在代码中管这样的操作叫drop_tokens，大家注意和MoE理论部分所说的drop token区分开。


（4）改进版All2All使用注意事项

在上面改进版All2All的讲解中，你可能已发现一个重要的点：虽然non-MoE采取了tp，但是MoE却没有用tp。
如果现在我把MoE也改成tp呢？g0存放 𝑒00 ，g1存放 𝑒01 ，g2存放 𝑒10 ，g3存放 𝑒11 ，即这里共2个专家，每个专家纵向切开为2，这种时候我们还需要采取drop tokens的方式吗？


答案是否定的，因为对于g0和g1来说，MoE层也被切开了，因此按照tp的方式，g0和g1上的输入各自过切开的MoE层后AllReduce的结果，才是最终结果。这时g0和g1上重复的输入数据是有实质意义的，我们不能drop。


deepspeed禅师，你看我们这样算悟了吗？

3.3 EP + DP + TP

（1）Non-MoE与MoE

现在我们再回到ep并行设置的例子上来，我们考虑对专家也做tp切分。实现这一点最简单的逻辑是让专家的tp切分方式和非专家的tp切分方式一致，这样省得我们再去对MoE层多写一套tp组的分布式设置。

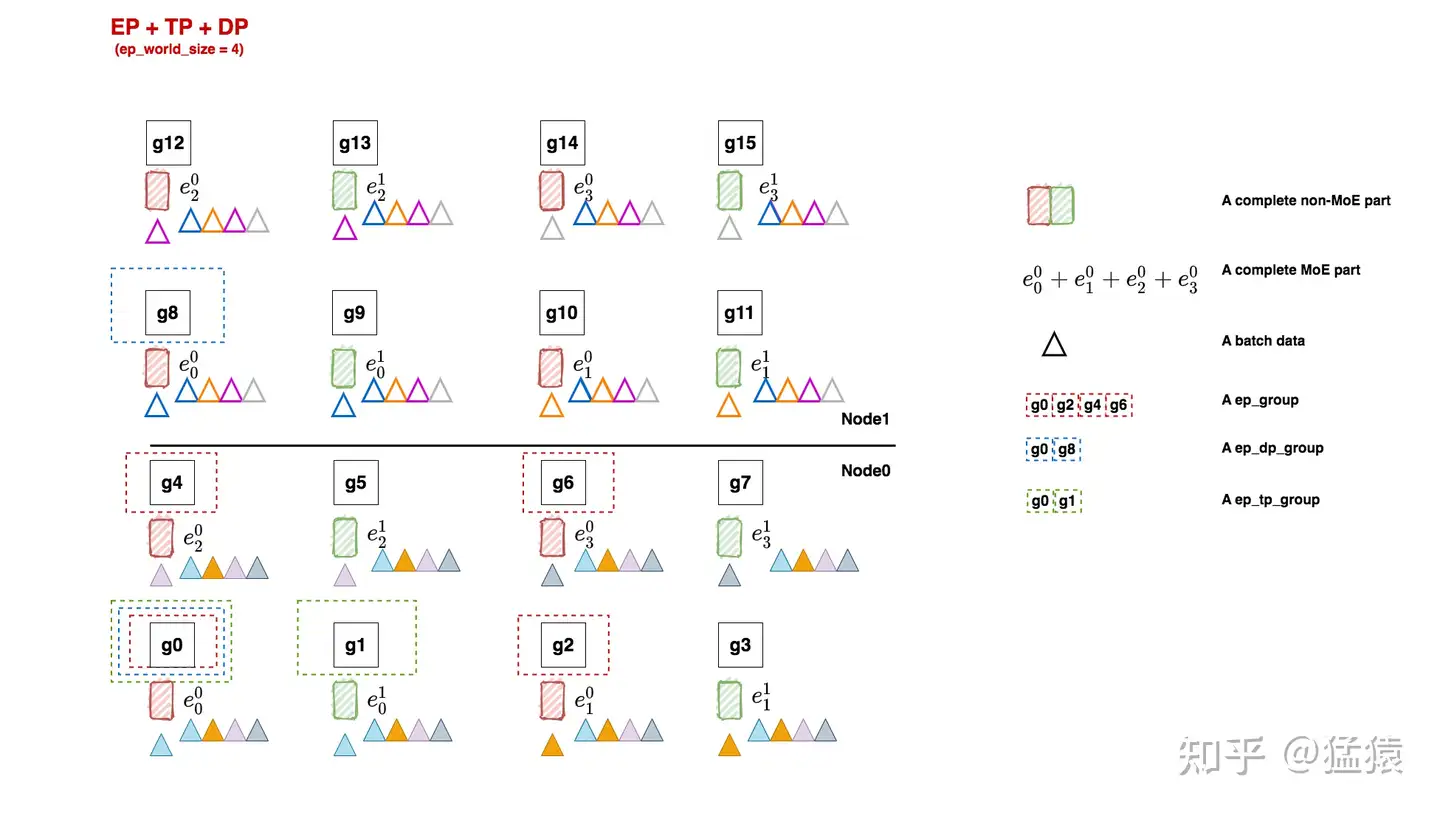
non-MoE组的并行设置和3.1一致，这里不再介绍，我们来看看MoE组的并行设置：

ep_world_size = 4，保持和3.1一致
ep_groups = [
            [g0, g2, g4, g6],
            [g1, g3, g5, g7],
            [g8, g10, g12, g14],
            [g9, g11, g13, g15]
           ]

ep_dp_world_size = 2
ep_dp_groups = [
                [g0, g8],
                [g1, g9],
                [g2, g10],
                [g3, g11],
                [g4, g12],
                [g5, g13],
                [g6, g14],
                [g7, g15]
                
# 复用non-MoE tp相关的并行设置
ep_tp_world_size = 2
ep_tp_groups = [...]

• ep_groups：在前面我们提过，每个ep_groups中的每个ep_group装下一套“完整的”专家，但我们也留了个坑，说明“完整”的含义需要留后讨论。现在我们就来看看这个坑。
  

  • 在deepspeed中，虽然每个ep_group内的专家都是被纵向切开的，但只要它涉及到所有的专家，就认为它是“完整的”

  • 在Megatron中，“完整”的含义就是参数完整，即g0~g7才被认为是一个ep_group。

定义不同，组内的通讯方式自然也不同。在deepspeed的定义下，ep_group内做的是all2all；在megatron的定义下，做的是ReduceScatter和AllGather（事实上Megatron的MoE实现就没有用到all2all）。这一点我们在源码讲解篇会来做比较。这里我先抛出我的结论：我认为deepspeed的ep_group设计是较好的，不仅操作上更符合直觉认知，还能避免重复数据发送（Megatron的实现方法会发送大量重复数据）。


（2）FWD与BWD

同样，我们通过描述1次FWD与BWD的过程，来说明各个group间是怎么运作的。

• 首先做FWD，数据过non-MoE层，因为采用了tp，所以相同tp组内的各卡输出一致，因此我们在图中将相同颜色的三角形放到对应的non-MoE参数块下。

• 继续做FWD，数据来到了MoE层。在例子中：
  

  • ep_group [g0, g2, g4, g6]和ep_group[g1, g3, g5, g7]内都各做1次all2all，将token发给对应的expert进行计算。

  • 计算完毕后，因为MoE层也是tp并行的，因此[g0, g1], [g2, g3], [g4, g5], [g6, g7]这几个tp组各自通过AllReduce取得完整的输出结果。

  • 然后ep_group [g0, g2, g4, g6]和ep_group[g1, g3, g5, g7]再做一次all2all，把计算完毕的数据发送回去，以便进入下一个non-MoE->MoE操作。我们在图中把这一步骤里各卡维护的expert所见过的batch数据画在对应的expert下面。

• 开始做BWD，数据来到MoE层。同一个ep_dp_group内的参数需要对梯度做AllReduce，例如图中[g0, g8]，这个group维护了相同的e，每个e都各自吃过4个batch的数据，联合起来刚好构成全局上的8个batch（牢记前文分布式训练的使命）.

• 继续做BWD，数据来到non-MoE层，来到大家熟悉的领域了，tp+dp模式下的BWD，就不需要多说了吧。

3.4 PP去哪里了

在上面的例子中，我们见过了ep+tp+dp的混合，你可能想问，pp也是一种常见的并行方式，它去哪里了呢？


在MoE中，PP这个维度比较特殊，大部分论文和开源代码实践中，一般不考虑/不讨论再对MoE部分做pp切分。deepspeed中更是强制把PP维度设为1，并在代码注释里表示不支持PP（我猜这可能和deepspeed的zero实现有关，体感上可能会加剧通讯量，但我没做仔细研究，给不出确切答案）。我个人认为，如果tp+dp已经能满足显存限制的话，就不需要再引入pp将模型切得更碎了。同时在MoE模型中，你会发现non-MoE的模型副本数和MoE的模型副本数是不一致的。例如3.2的例子中，non-MoE有8个模型副本，但是MoE只有两个模型副本（g0~g7, g8~g15），却也能实现8个完整的non-MoE + MoE模型副本的分布式训练效果。从这一点上看tp+dp形式的训练方式已经基本够用了。


但并不是说不能使用pp，Megatron中就支持pp的使用，我们来看下引入pp后的情况：

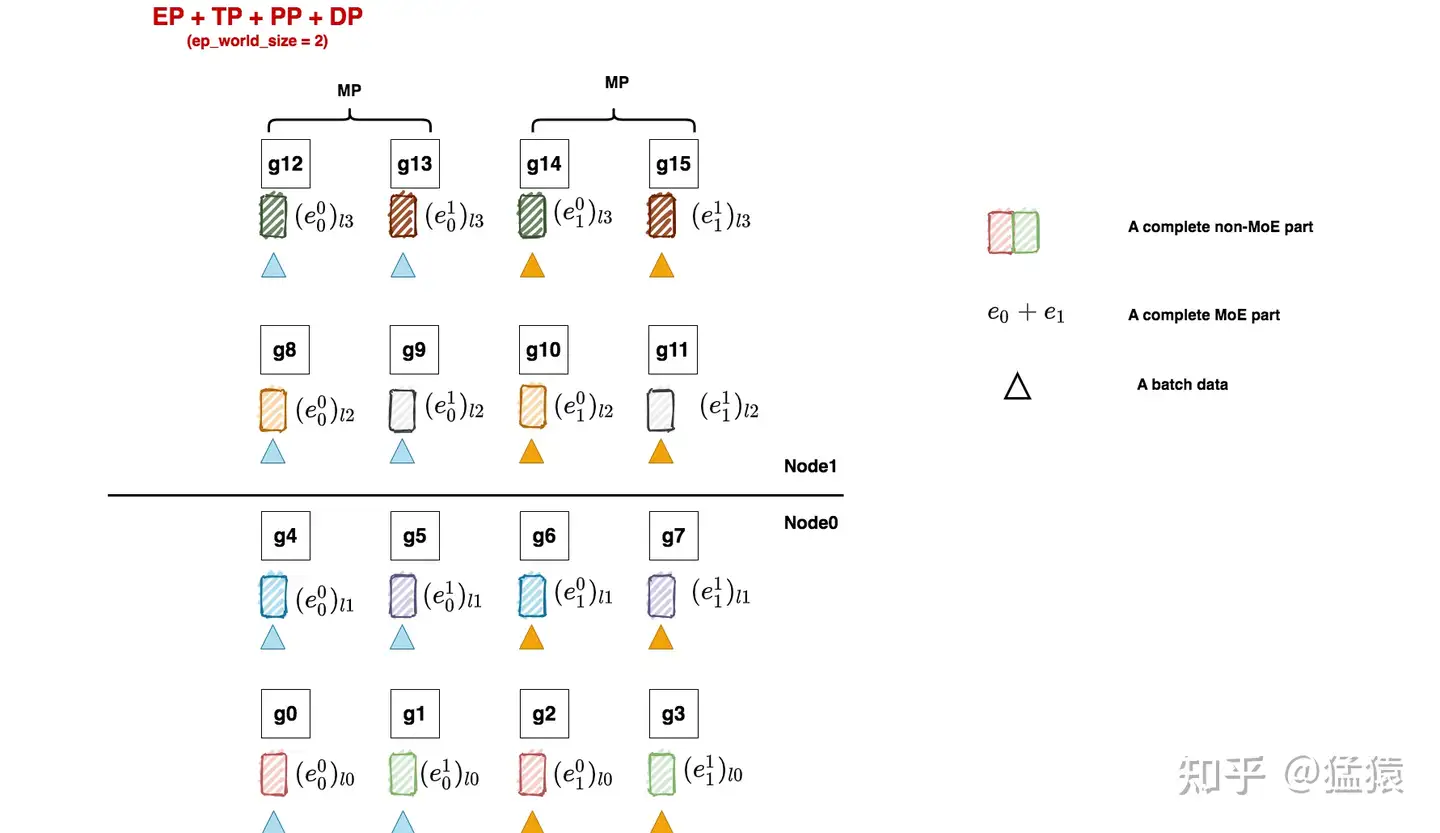
• non-MoE层采用tp + dp +pp并行（就是我们在Megatron解读中举的例子，是我们熟悉的味道）

• MoE层采用ep + tp +pp + dp，其中tp_group和tp_group直接复用non-MoE的设置

相信通过之前的讲解，大家已经能轻松看懂这张图了。这里只强调三点：

• ep_dp_groups = [[g0], [g1], [g2],...]，也就是每张卡单独组成了一个ep_dp_group（如果你觉得难以理解，就用前面说的每个e见过的batch来分析看看）

• ep_group = [[g0, g1, g2, g3], [g4, g5, g6, g7],...]，这个不难理解，想想上文说的Megatron对“完整的一套专家“的定义。这里特别说明下，你可能已经发现ep_world_size = 2，但这里每个ep_group占四块卡，这在Megatron中是正常的。在下篇源码解读中，我们会来看Megatron这样设计的意义。

• 需要满足dp_world_size % ep_world_size == 0，事实上这也是Megatron并行设置的前置条件（不管你有没有使用pp，因为Megatron强制MoE复用non-MoE的并行配制，在此基础上再引入和ep相关的并行）。一般而言，world_size = tp_world_size pp_world_szie dp_world_szie，如果你的MoE层复用了non-MoE的tp和pp，那么ep_world_size只能在dp_world_size上做切割了。