1.众数
出现频率最高的数
2.中位数
把样本值排序,分布在最中间的值;
样本总数为奇数时,中位数为第(n+1)/2个值;
样本总数为偶数时,中位数是第n/2个,第(n/2)+1个值的平均数。
3.平均数
所有数的总和除以样本数量;
现在大家接触最多的概念应该是平均数,但有时候,平均数会因为某些极值的出现收到很大影响。举个小例子,你们班有20人,大家收入差不多,19人都是5000左右,但是有1个同学创业成功了,年入1个亿,这时候统计你们班同学收入的“平均数”就是500万了,这也很好的解释了,每年各地的平均收入数据出炉,小伙伴们直呼给祖国拖后腿了,那是因为大家收入被平均了,此时,“中位数”更能合理的反映真实的情况。
变异性
1.四分位数
上面说到了“中位数”,把样本分成了2部分,再找个这2部分各自的“中位数”,也就把样本分为了4个部分,其中1/4处的值记为Q1,2/4处的值记为Q2,3/4处的值记为Q3。
2.四分位距 IQR=Q3-Q1
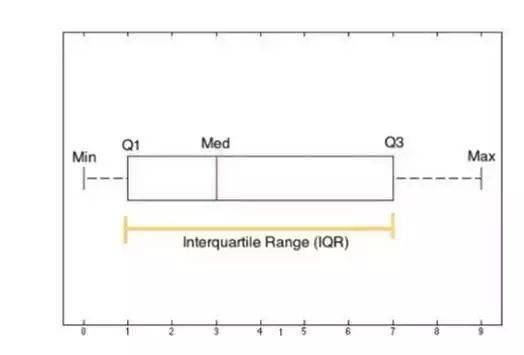
3.异常值
小于Q1-1.5(IQR)或者大于Q3+1.5(IQR);
对于异常值,我们在数据处理的环节就要剔除。
4.方差
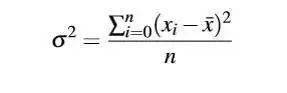
5.平方偏差
方差的算术平方根
6.贝塞尔矫正:修正样本方差
实际在计算方差时,分母要用n-1,而不是样本数量n。原因在于,比如在高斯分布中,我们抽取一部分的样本,用样本的方差表示满足高斯分布的大样本数据集的方差。由于样本主要是落在x=u中心值附近,那么样本如果用如下公式算方差,那么预测方差一定小于大数据集的方差(因为高斯分布的边沿抽取的数据也很少)。为了能弥补这方面的缺陷,那么我们把公式的n改为n-1,以此来提高方差的数值,这种方法叫贝塞尔矫正系数。
归一化
1.标准分数
一个给定分数 距离 平均数 多少个标准差?
标准分数是一种可以看出某分数在分布中相对位置的方法。
标准分数能够真实的反映一个分数距离平均数的相对标准距离。
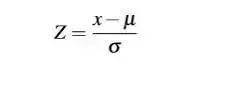
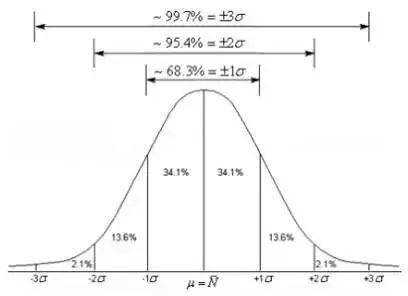
正态分布
1.定义
随机变量X服从一个数学期望为μ,方差为σ⊃2;的正态分布,记为N(μ,σ⊃2;)
随机取一个样本,有68.3%的概率位于距离均值μ有1个标准差σ内;
有95.4%的概率位于距离均值μ有2个标准差σ内;
有99.7%的概率位于距离均值μ有3个标准差σ内。
抽样分布
1.中心极限定理
设从均值为μ,方差为σ⊃2;的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值的抽样分布近似服从均值为μ、方差为σ⊃2;/n的正态分布。
2.抽样分布
设总体共有N个元素,从中随机抽取一个容量为n的样本,在重置抽样时,共有N·n种抽法,即可以组成N·n不同的样本,在不重复抽样时,共有N·n个可能的样本。每一个样本都可以计算出一个均值,这些所有可能的抽样均值形成的分布就是样本均值的分布。但现实中不可能将所有的样本都抽取出来,因此,样本均值的概率分布实际上是一种理论分布。数理统计学的相关定理已经证明:在重置抽样时,样本均值的方差为总体方差的1/n。
举个例子:
48盆MM豆,计算出每盆有几个蓝色的MM豆,48个数据构成了总体样本。然后随机选择五盆,计算五盆中含有蓝色MM豆的平均数,然后反复进行了50次。这就是n为5的样本均值抽样。
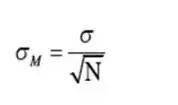
估计
1. 误差界限
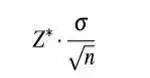
2. 置信度
我们有百分之多少确信总体中的值落在一个特定范围内;
一般情况下,取95%的置信度就可以。
3. 置信区间
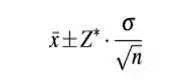
假设检验

1.问题:什么是显著性水平?
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率。

2. 如何选择备选检验和零假设?
一个研究者想证明自己的研究结论是正确的,备择假设的方向就要与想要证明其正确性的方向一致;
同时将研究者想收集证据证明其不正确的假设作为原假设H0。
T检验
1. 主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布。
流程如下:
是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著;
一般检验水准α取0.05即可;
计算检验统计量的方法根据样本形式不同。
2. 独立样本T检验:
现在要分析男生和女生的身高是否相同两者的主要区别在于数据的来源和要分析的问题。
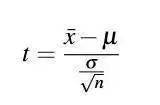
问题:为什么T检验查表时候要n-1?
样本均值替代总体均值损失了一个自由度
3. 配对样本t检验
分析人的早晨和晚上的身高是否不同,于是找来一拨人测他们早上和晚上的身高,这里每个人就有两个值,这里出现了配对。
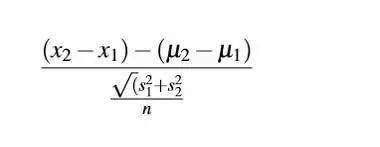
样本误差(Standard Error)
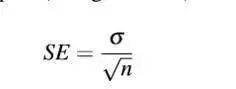
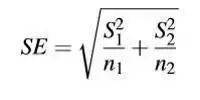
4. 合并方差
当样本平均数不一样,但实际上认为他们的方差是一样的时候,需要合并方差。
不要被公式吓到,他的本质是两个样本方差加权平均。

-END-

