前言

信息论在1948年由香农提出，此后在各个工程技术领域都有广泛应用。

在机器学习领域，当然也包括自然语言处理领域，信息论是一个基础内容。离开信息论想要讨论清楚NLP是非常困难的。

因此，本文主要是为了给下一步的自然语言处理做理论基础铺垫，尽量不涉及公式，而是从直观的角度来理清信息论的直觉逻辑，这比罗列公式更有助于加深理解。

信息论基本模型

既然提到信息二字，那么就一定意味着信息的传递，有信息发送方以及信息接收方。若信息是停留在某处完全静止，则无所谓信息论。如下图所示。

信息论的基本通信模型，以打电话为例展示

这样的一个信息传递的过程，和打电话非常相似。也就是说，实际上信息论是嵌入在通信系统上的一个理论框架，最初是用来解决通信问题的。当然，信息论在各个领域的扩展和应用，都是将问题抽象为一个通信问题展开的。神经网络等等各种模型，实际上也可以看作是一种通信系统，这个随后展开。

信息传递模型的进一步抽象

根据上图男孩和女孩打电话的示意图，我们可以将其看作一个基本的通信系统，其主要包括如下几个部件：

男孩：信息的发送方，他通过语言向女孩传递信息内容，比如，他说的话是“我喜欢你，你喜欢我吗？”

女孩：信息的接收方，她通过同样的语言接收男孩所说的话。

电话线：信息介质，就像声音的传递需要机械震动一样，信息的传递是将语言转化为电话线的震动来进行信息的传递，当然，光、声音、无线电播都是可以传递的媒介。这里就有一个传递准确性的问题，也就是，女孩是否能真的听清男孩所说话内容的问题，在有杂音的情况下，女孩所听内容可能是“我喜欢你，喜欢我吧。”

语言：信息的编码。男孩所传递的信息，不仅仅可以用中文进行表达，还可以用英语、法语做传递，实际上传递的信息内容是一样的，但是采用的语言不同，这里，语言并非信息本身，而是一种对信息的编码。编码的方式是多种多样的。

信息熵

信息熵又称信息量，他是衡量在通信过程中，传递了多少信息。

传递了多少信息，是个非常抽象的东西，还是以上面男孩对女孩说话为例，我们可以定义男孩对女孩说了一句话，这句话定义为X。X是一个未知数，站在女孩的角度，她并不知道男孩要说什么话，也就是说，X可看作是一个随机变量。

如果男孩说：“太阳从东边升起”。估计女孩听了会翻白眼，这不是废话吗？一点信息量都没有。是的，这句话从信息论角度而言，就是一点信息量都没有，因为，太阳每天都从东边升起，这是万年不变的常识，X这个随机变量，其概率为1，也就是这件事必然发生，此时信息量为0。

如果男孩说：“四川遭遇了有气象观测记录以来的最干旱高温的夏天。”此时则是信息量非常大的一句话，女孩听了会震惊，男孩说了会流泪。原因就在于，四川遭遇数十年一遇的高温和干旱，这个概率实在是太低了，怎么算，也有数十分之一吧，就按五十分之一算，这个结果就是概率值 0.02。当一件特别不可能发生的事情发生的时候，这个信息量就是非常大的。

从上面的过程，我们大致可以了解到，信息量所衡量的东西，就是信息接收方，对信息直观的震惊程度。这也非常符合我们的直觉。

且公式的定义也是由概率出发定义而得。

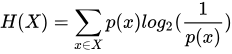
这个定义里，正好符合上述信息量随概率变化的要求。然而，满足直观变化要求的函数非常多，这里为什么必须是 log 函数呢？

想象这里的X不再是一句描述性的话，而是单纯一个硬币的事情，出现正面的概率和出现反面的概率都是二分之一，那么可以计算得到信息量为1。

如果这个任务是分别投掷两枚硬币，那么同时出现正面的概率就是四分之一，计算信息量就可以得到为2。

这里就出现一个现象，硬币多投了一次，信息量也就多了1。如果是三枚硬币分别投掷，则信息量就变成了3。

换句话说，投掷次数和信息量是紧密相关的，是加性的，而概率值和投掷次数之间是乘性的，我们很直观的可以想到，log 函数族可以解决加性和乘性的转换，则信息量（信息熵）的定义公式，也就是如上所示了。

信息熵是信息量中的核心内容，并且这个概念和通信系统的抽象模型是紧密绑定的，但是似乎论述到这里，信息熵的概念仅仅和一个随机变量有关系。这里需要强调的是，这个随机变量本身就是通信信息的抽象，也就是，不论这里概念如何转换，只要出现了一个随机变量，那么一定意味着，我们可以想象，这个论述是围绕着一个接收者接收信息的。

交叉熵

我们再举一个买彩票中奖的例子。比如，中彩票概率是0.0001，而不中是 0.9999（现实似乎比这要更难中奖，当然了，社会上还爆出了一些中奖者很多都是彩票机构员工的新闻）。中奖的概率太低了，这是我们每一个人都默认的一个概率情况。

有一个小伙子叫小北航，他也知道这个中奖概率低得可怜，玩票性质买了一次彩票，不中，小北航一点都不吃惊（得到的信息量低）；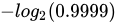

第二次，小北航又买了一次，中！小北航非常开心（得到的信息量高，）；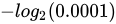

第三次，小北航又买了一次，又中了！小北航开始狂喜，这比地球爆炸的概率还低啊，居然让我给赶上了！连续两次中奖的信息量极其大，是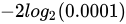，这已经相当爆炸了。

连中两次中奖之后，小北航就会产生怀疑，为什么我能连中两次？太出乎预料了！（得到的信息量大的可怕）他怀疑是不是这个彩票系统有问题（即，发生在他身上的真实的中彩概率不是0.0001）。

经过调查才发现，彩票中心主任是小北航他爸，所以小北航很容易中奖（他爸给他设定的真实中奖概率是0.3，不中的概率是0.7）；这样连中两次也不奇怪了。

所以，本以为中奖概率是0.0001，去进行试验，大呼吃惊，结果发现真实的概率是0.3，这个大呼吃惊的吃惊程度就是交叉熵。

反之，如果小北航早就知道了自己的老爸暗中安排了，连中两次似乎也没有多么神奇嘛！（0.3* 0.3，不吃惊，信息量少）

交叉熵的直观含义就是：用自以为的分布去观测一个随机变量，结果发现得到数据多少令自己吃惊，此时得到的信息量就是交叉熵。

更直白的说，交叉熵本质就是，真实分布（后验分布）出乎预料已知猜测的分布（先验分布）的程度。

把交叉熵放在通信模型中，它表示，接收方（图中女孩）接收到的信息，相对于它预期的吃惊程度。

再举一个例子，加深理解。

前述“太阳从东边升起”，是条信息量为0的信息。我们知道刘慈欣的流浪地球，地球受到各种影响，导致太阳从西边升起（当前真实分布），而此时，生活在地下的人们还不知道呢，以为还从东边升起（先验的预期分布），过了一段时间，这个消息被发布，全世界的人都吃了一惊。这个吃惊就是交叉熵。公式表达为

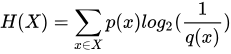
其中p概率分布是事件真实发生的概率分布，而q概率分布则是先验的分布，从直观上来讲，公式的直观含义就是，用真实概率分布，与相应的人们心中默认的先验吃惊程度求期望。

相对熵

相对熵的概念基本上由交叉熵引申而来。根据交叉熵的定义，我们知道，交叉熵是一个十分绝对的值，那么相对熵就是一个相对的值。用事件X发生后的后验交叉熵，减去先验默认的信息熵，就是相对熵。相对熵又称KL散度（Kullback-Leibler Divergence）。

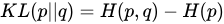
由此可知，相对熵衡量的是一个相对的吃惊程度，如果先验概率分布（人们心中默认的分布）与真实分布差距过大，则相对熵就变大，反之两者极为相似，则相对熵就很小。

交叉熵与神经网络的关系

在各类神经网络中，输入输出都是可以采用概率分布来表示的。而尤其在输出部分，假设我们的输出是个分类任务，这个事件可以起名叫做Y，Y是一个随机变量，它有k个分类的类别。为了方便理解，我们进一步假设这个分类任务是对一篇文本做类型分类，类别有政治、经济、娱乐、社会、科技、自然地理等类型。

那么，真实的标注语料中的Y有一个概率分布p，而神经网络模型预测出来的Y也有一个概率分布q。

此时就很容易了，我们可以把交叉熵通过一个样本、一个样本这样计算出来，得到一个值，并将其当作一个损失函数来训练这个模型。

如果对于一个样本，其真实标注的分类的标签和模型预测的标签概率分布差距越大，则其交叉熵值就越大，从通信角度而言，以本篇博客为例，本来我们默认这个分类的类别应该是科技类文本，那么我们先验的分布实际是[0,...0,1,0,...0]，其中，1代表科技类别，而其它的0代表所有的其它类别。而模型预测的后验分布为[0.1, ..., 0.04,0.2,0.4..., 0.01]，在这里，科技类对应的概率是 0.2，而其它的类别对应了不同的概率值，此时，两个概率的差异，即交叉熵值，实际上就表示了一种震惊程度，本来文本是科技类，模型却分类到了别的类别上去！

总结

信息论与NLP，以及神经网络的关系当然不仅仅局限于一个交叉熵。除此之外，神经网络还可以看作一个通信的信道噪声模型、信源编码模型等等，从不同的角度看待模型都会得到不同的解释和理解。之后根据情况将继续更新相应的内容。