浮点数的数据格式
根据 IEEE754 的标准定义:浮点数的数据格式可以分为最常见的单精度(32位)和双精度(64位)格式,以及半精度(16位)、四精度(128位)和扩展精度格式。
单精度浮点数(Single-Precision Floating-Point):在计算机编程中常用float表示:
通常占用 32 位(4 个字节)的存储空间
在IEEE 754标准中,单精度浮点数由1位符号位、8位指数位和23位尾数位组成。
一个 4 个字节(32 位)的单精度浮点数可以表示大约 ±3.4 x 10^38 的范围内的小数。这个范围非常大,可以满足大部分应用程序对小数值的存储需求。同时,单精度浮点数通常提供6-7 位有效数字的精度。
双精度浮点数(Double-Precision Floating-Point):在计算机编程中常用double表示,如:
//定义一个圆形类,其中包括了圆周率常量和半径变量
package com.buptnu.demo;
public class CCircle {
final double PI = 3.141592;
double radius;
}通常占用 64 位(8 个字节)的存储空间
在IEEE 754标准中,双精度浮点数由1位符号位、11位指数位和52位尾数位组成。
一个 8 个字节(64 位)的双精度浮点数可以表示大约 ±1.7 x 10^308 的范围内的小数。这个范围非常大,可以满足大部分应用程序对小数值的存储需求。同时,双精度浮点数通常提供大约 15-16 位有效数字的精度
注:-6.02×10^23 这个数,“-"表示符号位,用于表示正负,6.02表示尾数,10^23表示指数
在程序设计和科学计算中,单精度浮点数通常用于那些不需要极高精度计算的场合,因为与双精度浮点数相比,单精度浮点数在计算速度和占用存储空间方面具有一定的优势。然而,当需要更高精度和更大范围的数值时,通常会使用双精度浮点数(64位),尽管这会以牺牲一定的性能和增加存储需求为代价
其余三种数据格式
扩展精度浮点数(Extended Precision):
此类别下的具体格式可能会根据不同的硬件和软件实现有所变化。通常,它们提供比双精度更高的精度和/或更广的范围。
例如,在某些实现中,扩展精度可能使用80位(10字节)或更多位来表示一个浮点数。
半精度浮点数(Half Precision):
使用16位(2字节)来表示一个浮点数。
包括1位符号位、5位指数位和10位尾数位。
半精度格式主要用于特定的应用领域,如图形处理和深度学习,其中计算效率和存储效率可能比数值精度更加重要。
四精度浮点数(Quadruple Precision):
使用128位(16字节)来表示一个浮点数。
包括1位符号位、15位指数位和112位尾数位。
四精度提供了极高的数值精度,适用于科学计算中需要极高精度的计算场景。
IEEE 754标准的这些不同格式使得浮点数在各种计算需求中具有灵活性,从而可以根据具体的应用场景选择最合适的数据精度和大小。
注意:上面提到的是属于不同的的数据格式,并不是浮点数的分类,是用于表示各种类型的浮点数,包括规约数、非规约数、零、无穷大和NaN
根据IEEE 754标准,浮点数主要可以被分为以下几类:
规约数(Normalized numbers):
这是最常见的浮点数类型,用于表示除零以外的大多数数值。
规约数的表示确保了尾数(mantissa)的最高位隐含为1(对于二进制浮点数而言)。这意味着实际的尾数比存储的尾数多一个最高位的1,从而提高了表示的有效性。
指数部分既可以是正数也可以是负数,通过一个偏移量(或称为偏置)来表示。
非规约数(Denormalized numbers,也称为次正规数):
这类浮点数主要用于表示非常接近于0的正数和负数。
非规约数的指数固定为最小值,而尾数不假定隐含的最高位为1,这允许表示比规约数更接近于零的数值。
主要作用是提供了一种平滑的过渡方式,使得数值可以渐进到0,避免了硬阈值导致的突变,这一点在数值计算中非常重要。
零(Zero):
IEEE 754标准定义了正零和负零,尽管在大多数运算中它们的行为是相同的,但在某些情况下,区分正负零可以提供更多的数学灵活性(比如在处理极限或导数时)。
=无穷大(Infinity):
分为正无穷大和负无穷大,用于表示超出浮点数表示范围的大数值,比如溢出的结果。
在数学运算中,无穷大的引入允许某些运算可以继续进行,而不是简单地失败。
NaN(Not a Number,不是一个数字):
用于表示那些无法定义或不适用于常规浮点数的结果,如0除以0、无穷大减去无穷大等。
NaN本身有多种形式,可以携带额外信息来指示导致NaN结果的特定原因。
这些分类使得IEEE 754标准的浮点数能够灵活地表示和处理广泛的数值,包括非常特殊的情况,同时在各种计算场景中保持数学上的一致性和可预测性。
半精度是英伟达在2002年搞出来的,双精度和单精度是为了计算,而半精度更多是为了降低数据传输和存储成本。
很多场景对于精度要求也没那么高,例如分布式深度学习里面,如果用半精度的话,比起单精度来可以节省一半传输成本。考虑到深度学习的模型可能会有几亿个参数,使用半精度传输还是非常有价值的。
Google的TensorFlow就是使用了16位的浮点数,不过他们用的不是英伟达提出的那个标准,而是直接把32位的浮点数小数部分截了。据说是为了less computation expensive。。。
比较下几种浮点数的layout:
双精度浮点数:
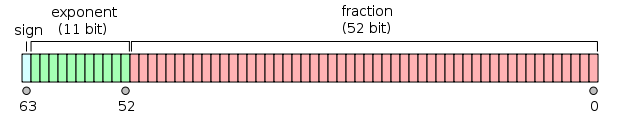
单精度浮点数:

半精度浮点数:
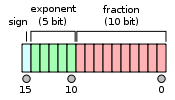
它们都分成3部分,符号位,指数和尾数。不同精度只不过是指数位和尾数位的长度不一样。
解析一个浮点数就5条规则:
如果指数位全零,尾数位是全零,那就表示0
如果指数位全零,尾数位是非零,就表示一个很小的数(subnormal),计算方式 (−1)^signbit × 2^−126 × 0.fractionbits
如果指数位全是1,尾数位是全零,表示正负无穷
如果指数位全是1,尾数位是非零,表示不是一个数NAN
剩下的计算方式为 (−1)^signbit × 2^(exponentbits−127) × 1.fractionbits 常用的语言几乎都不提供半精度的浮点数,这时候需要我们自己转化。
具体可以参考Numpy里面的代码:
https://github.com/numpy/numpy/blob/master/numpy/core/src/npymath/halffloat.c#L466
当然按照TensorFlow那么玩的话就很简单了(~摊手~)。
参考资料:
https://en.wikipedia.org/wiki/Half-precision_floating-point_format
https://en.wikipedia.org/wiki/Double-precision_floating-point_format
https://en.wikipedia.org/wiki/Single-precision_floating-point_format

