图解大模型训练之：数据并行上篇(DP, DDP与ZeRO)

一、切分权重

设输入数据为X，参数为W。X的维度 = (b, s, h)，W的维度 = (h, h')。其中：

• b：batch_size，表示批量大小

• s：sequence_length，表示输入序列的长度

• h：hidden_size，表示每个token向量的维度。

• h'：参数W的hidden_size。

则每次forward的过程如下：

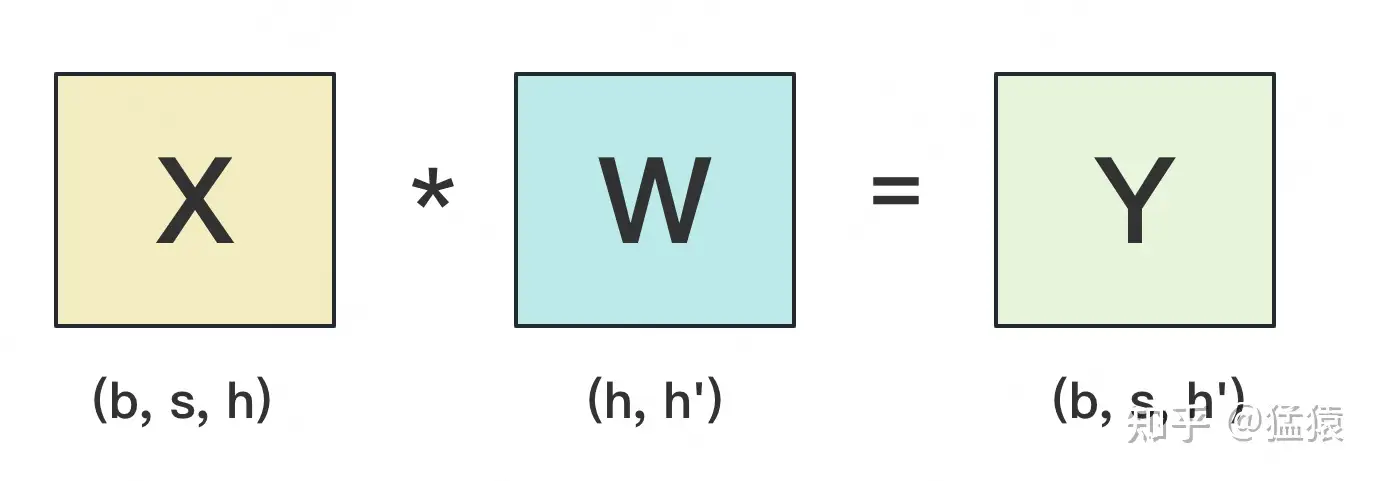
为画图方便，图中所绘是b=1时的情况。
假设现在W太大，导致单卡装不下。我们需要把W切开放到不同的卡上，则我们面临三个主要问题：

• 怎么切分W。

• 切完W后，怎么做forward。

• 做完forward后，怎么做backward，进而求出梯度，更新权重。

一般来说，我们可以沿着W的行（h维度），或者列（h'维度）切分W。下面我们分别介绍这两种切割办法，并说明它们是如何做forward和backward的。

1.1 按行切分权重

(1) forward

我们用N来表示GPU的数量。有几块GPU，就把W按行维度切成几份。下图展示了N=2时的切割方式：

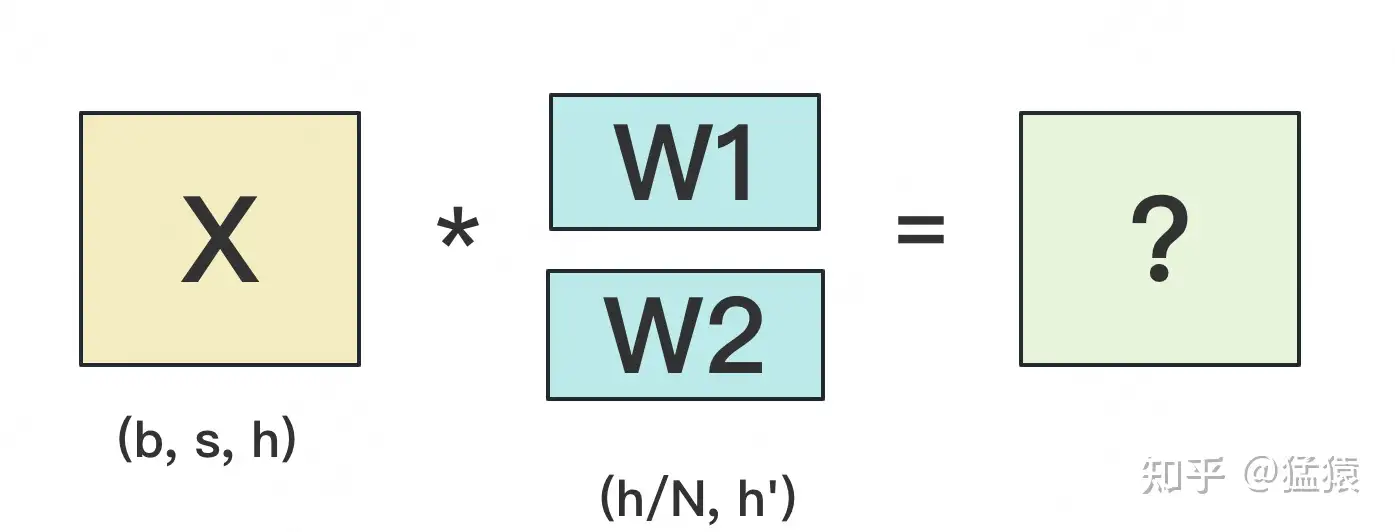
W按照行维度切开后，X的维度和它不对齐了，这可怎么做矩阵乘法呢？很简单，再把X“按列切开”就行了，如下图所示：

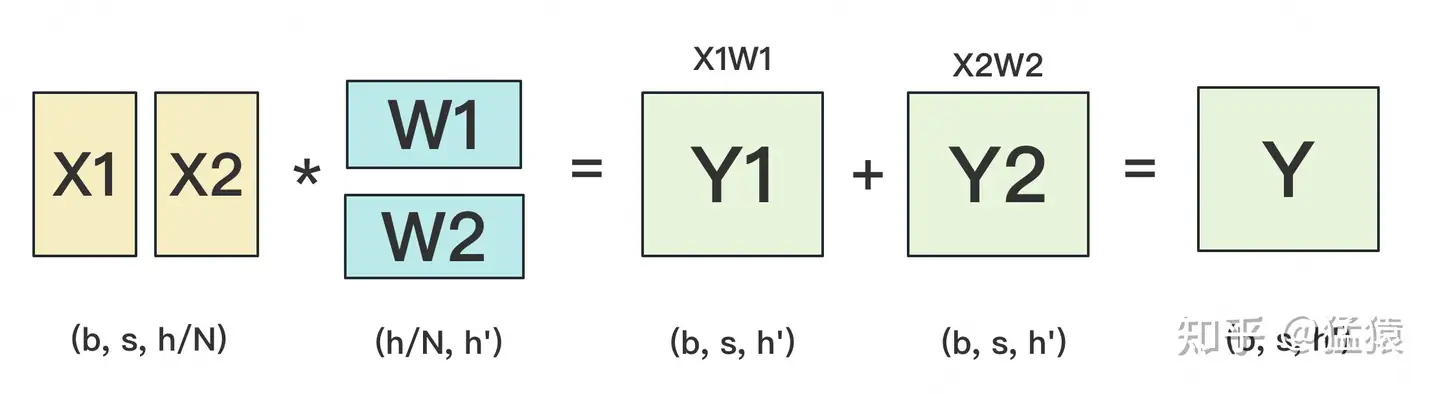
(2) backward

做完forward，取得预测值Y，进而可计算出损失L，接下来就能做backward了。我们重画一下forward的过程，并在其中加入backward的部分，整体流程图如下：

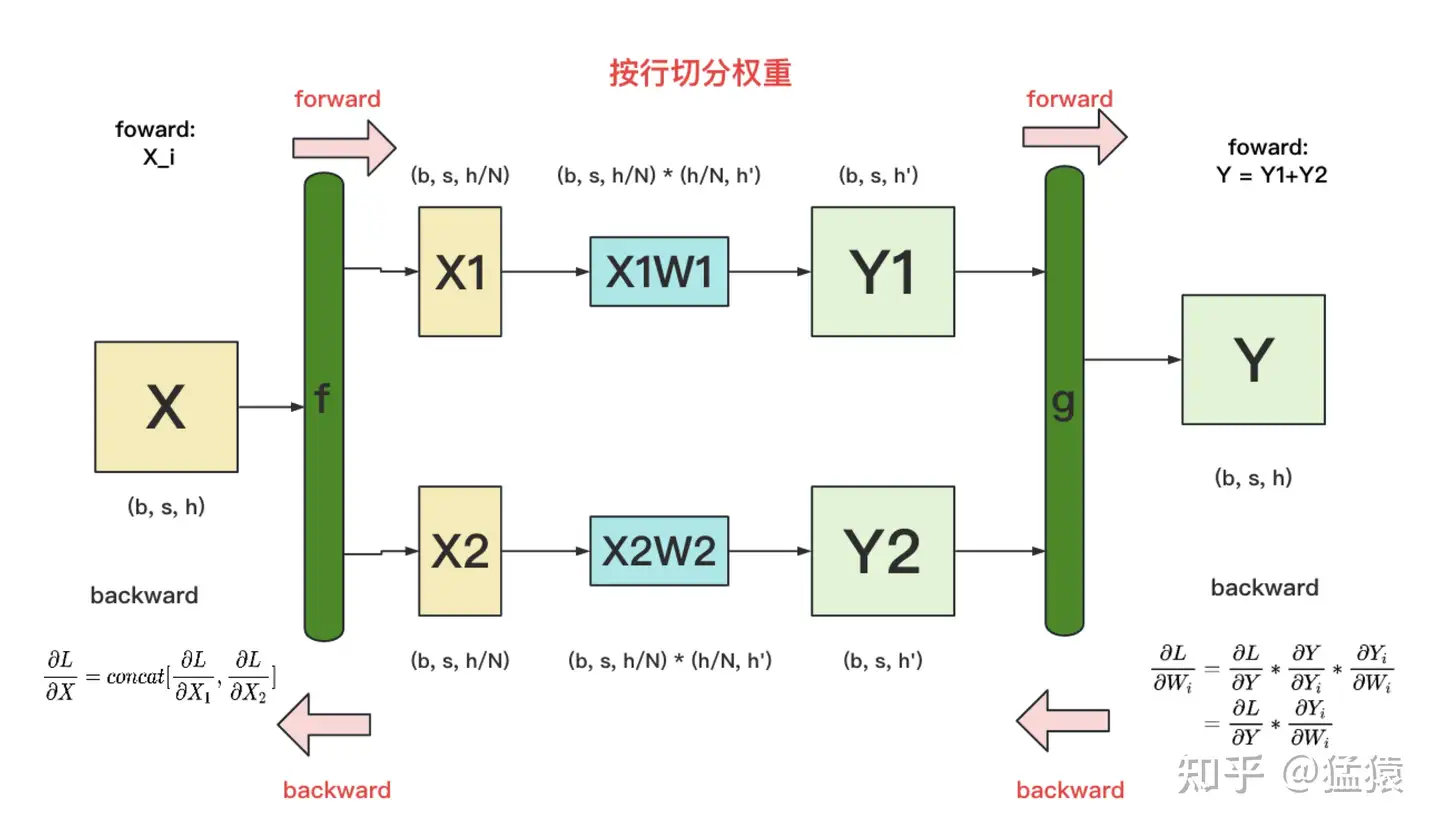
• f 和 g：分别表示两个算子，每个算子都包含一组forward + backward操作。forward操作已讲过，不再赘述。

• 图中的每一行，表示单独在一块GPU上计算的过程

• g 的backward：假定现在我们要对 𝑊𝑖 求梯度，则可推出 ∂𝐿∂𝑊𝑖=∂𝐿∂𝑌∗∂𝑌∂𝑌𝑖∗∂𝑌𝑖∂𝑊𝑖=∂𝐿∂𝑌∗∂𝑌𝑖∂𝑊𝑖 ，也就是说，只要把 ∂𝐿∂𝑌 同时广播到两块GPU上，两块GPU就可以独立计算各自权重的梯度了。

• f 的backward：在上图中，我们只画了模型其中一层的计算过程。当模型存在多层时，梯度要从上一层向下一层传播。比如图中，梯度要先传播到X，然后才能往下一层继续传递。这就是f 的backward的作用。这里也易推出， ∂𝐿∂𝑋=𝑐𝑜𝑛𝑐𝑎𝑡[∂𝐿∂𝑋1,∂𝐿∂𝑋2]

1.2 按列切分权重

（1）forward

按列切分权重后，forward计算图如下：

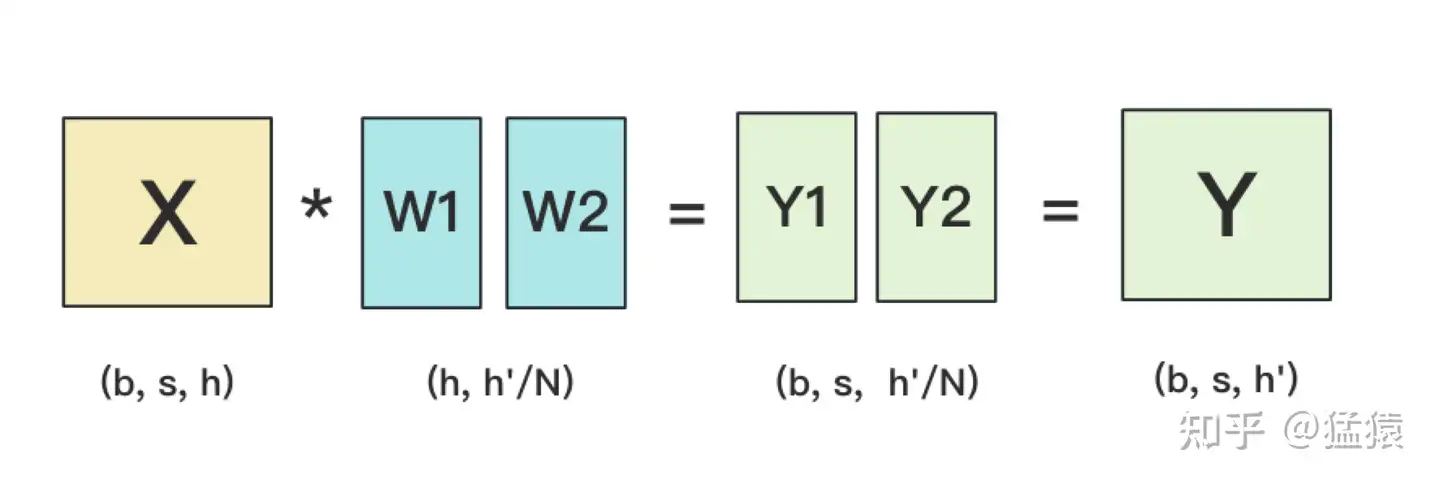
（2）backward

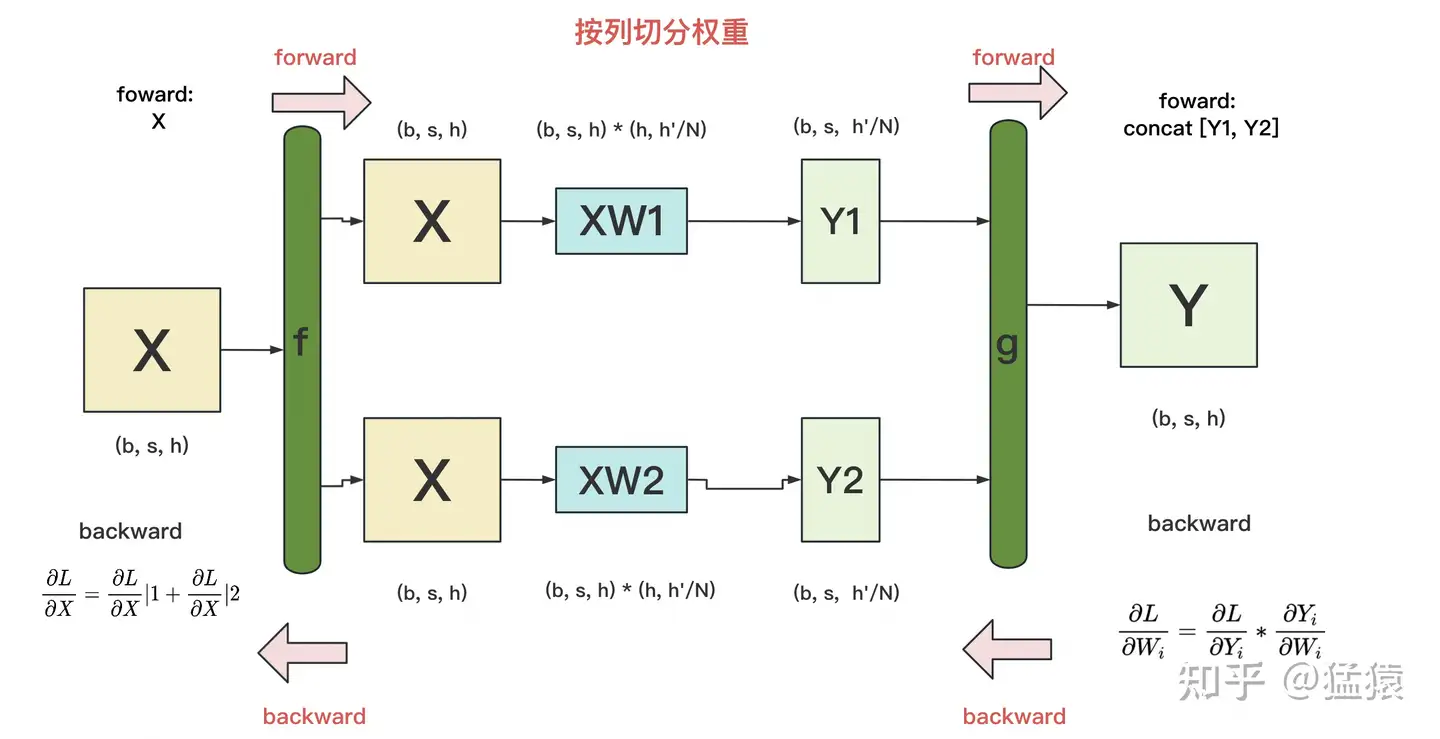
• g的backward：易推出 ∂𝐿∂𝑊𝑖=∂𝐿∂𝑌𝑖∗∂𝑌𝑖∂𝑊𝑖

• f 的backward：因为对于损失L，X既参与了XW1的计算，也参与了XW2的计算。因此有 ∂𝐿∂𝑋=∂𝐿∂𝑋|1+∂𝐿∂𝑋|2 。其中 ∂𝐿∂𝑋|𝑖 表示第i块GPU上计算到X时的梯度。

现在，我们已分别介绍完了“按行”和“按列”切分权重的方法。在Megatron-LM中，权重的切分操作就是由这两个基础算子组合而成的。接下来，针对Transformer模型，我们依次来看在不同的部分里，Megatron-LM是怎么做切分的。

二、MLP层

2.1 MLP层的张量模型并行计算方法

MLP层构造最简单，所以我们先来看它。MLP层计算过程如下图：

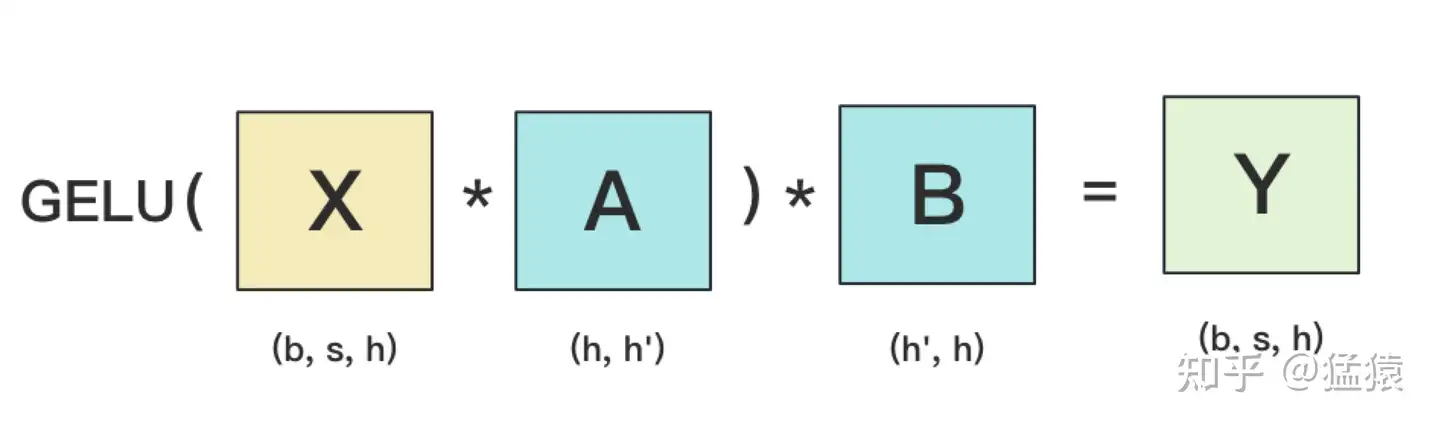
其中，GELU是激活函数，A和B分别为两个线性层。在Transformer里，一般设h' = 4h。假设现在有N块GPU，我们要把MLP层的权重拆到上面做计算，要怎么拆分呢？Megatron提供的拆分办法如下：

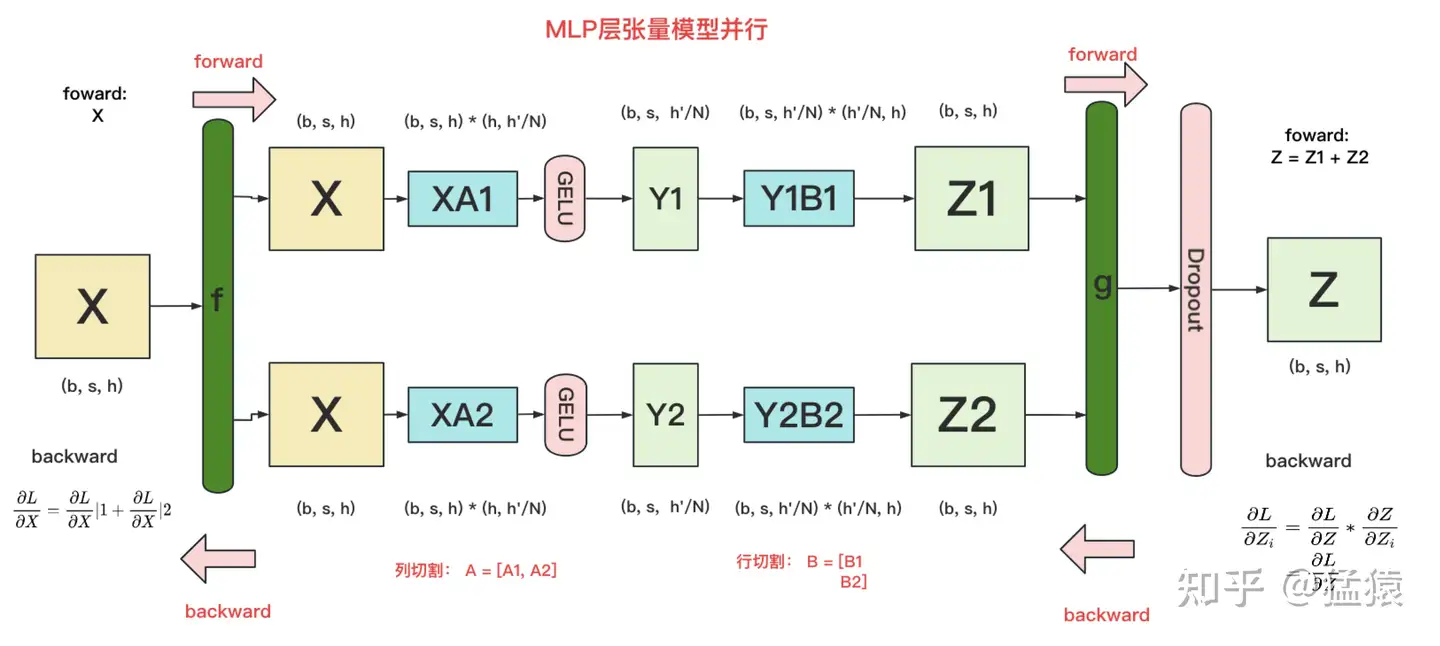
在MLP层中，对A采用“列切割”，对B采用“行切割”。

• f 的forward计算：把输入X拷贝到两块GPU上，每块GPU即可独立做forward计算。

• g 的forward计算：每块GPU上的forward的计算完毕，取得Z1和Z2后，GPU间做一次AllReduce，相加结果产生Z。

• g 的backward计算：只需要把 ∂𝐿∂𝑍 拷贝到两块GPU上，两块GPU就能各自独立做梯度计算。

• f 的backward计算：当当前层的梯度计算完毕，需要传递到下一层继续做梯度计算时，我们需要求得 ∂𝐿∂𝑋 。则此时两块GPU做一次AllReduce，把各自的梯度 ∂𝐿∂𝑋|1 和 ∂𝐿∂𝑋|2 相加即可。

为什么我们对A采用列切割，对B采用行切割呢？这样设计的原因是，我们尽量保证各GPU上的计算相互独立，减少通讯量。对A来说，需要做一次GELU的计算，而GELU函数是非线形的，它的性质如下：

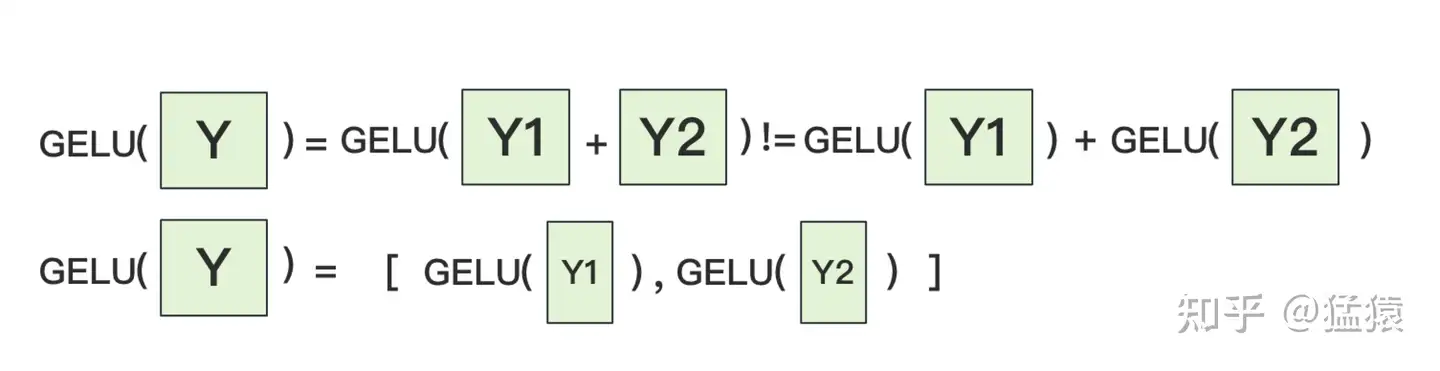
也就意味着，如果对A采用行切割，我们必须在做GELU前，做一次AllReduce，这样就会产生额外通讯量。但是如果对A采用列切割，那每块GPU就可以继续独立计算了。一旦确认好A做列切割，那么也就相应定好B需要做行切割了。

2.2 MLP层的通讯量分析

由2.1的分析可知，MLP层做forward时产生一次AllReduce，做backward时产生一次AllReduce。在之前的文章里我们讲过，AllReduce的过程分为两个阶段，Reduce-Scatter和All-Gather，每个阶段的通讯量都相等。现在我们设每个阶段的通讯量为 Φ ，则一次AllReduce产生的通讯量为 2Φ 。MLP层的总通讯量为 4Φ 。
根据上面的计算图，我们也易知， Φ=𝑏∗𝑠∗ℎ

三、Self-Attention层

现在，我们来看稍微复杂一点的self-attention层切割方式（Transformer中Encode和Decoder之间还有做cross-attention，但计算逻辑和self-attention一致，因此这里只拿self-attention举例）。
首先，我们快速过一下multi-head attention层的参数构造。对Transformer Attention不熟悉的读者，可以参见之前写的这篇文章，其中有详细的图解。

3.1 Multi-head Attention的计算方法

当head数量为1时，self-attention层的计算方法如下：

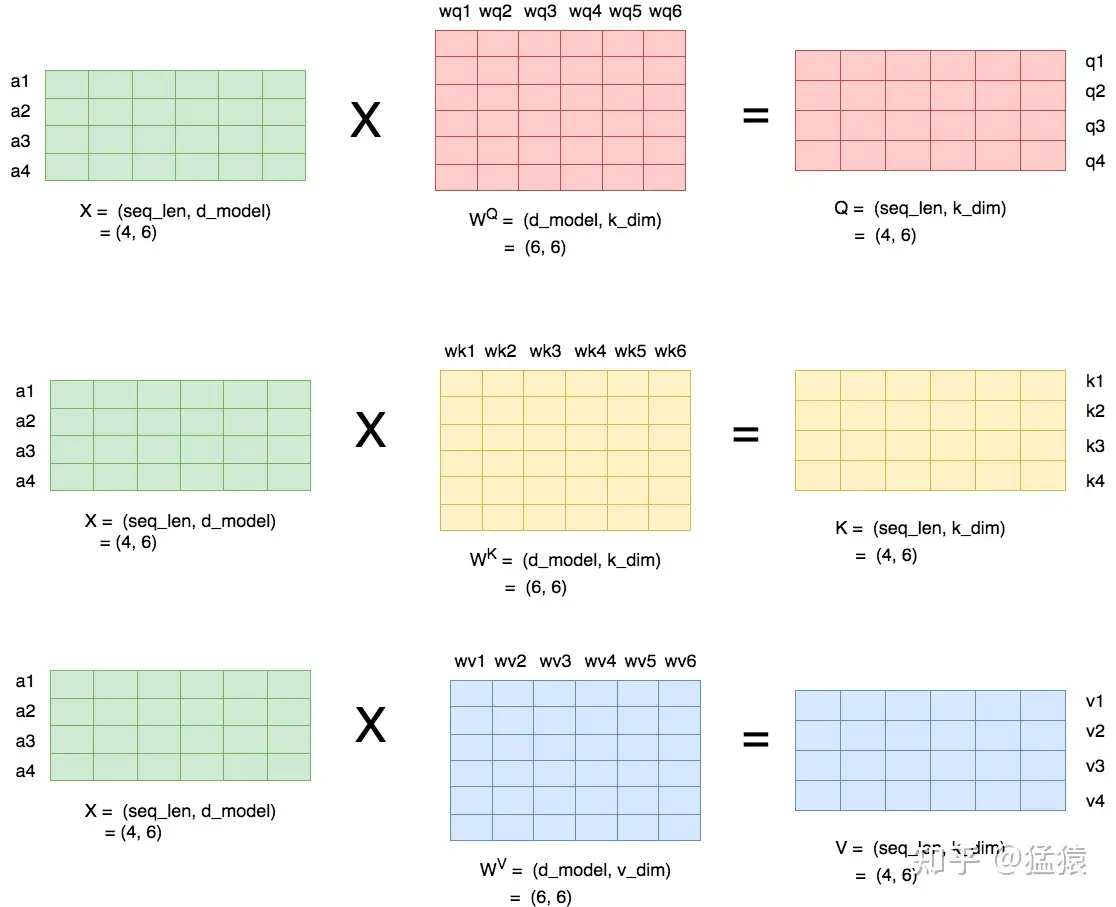
• seq_len，d_model分别为本文维度说明中的s和h，也即序列长度和每个token的向量维度

• 𝑊𝑄,𝑊𝐾,𝑊𝑉 即attention层需要做训练的三块权重。

• k_dim，v_dim满足： 𝑘_𝑑𝑖𝑚=𝑣_𝑑𝑖𝑚=𝑑_𝑚𝑜𝑑𝑒𝑙//𝑛𝑢𝑚_ℎ𝑒𝑎𝑑𝑠=ℎ//𝑛𝑢𝑚_ℎ𝑒𝑎𝑑𝑠

理清了单头，我们来看多头的情况，下图展示了当num_heads = 2时attention层的计算方法。即对每一块权重，我们都沿着列方向（k_dim）维度切割一刀。此时每个head上的 𝑊𝑄,𝑊𝐾,𝑊𝑉 的维度都变成(d_model, k_dim//2)。每个head上单独做矩阵计算，最后将计算结果concat起来即可。整个流程如下：

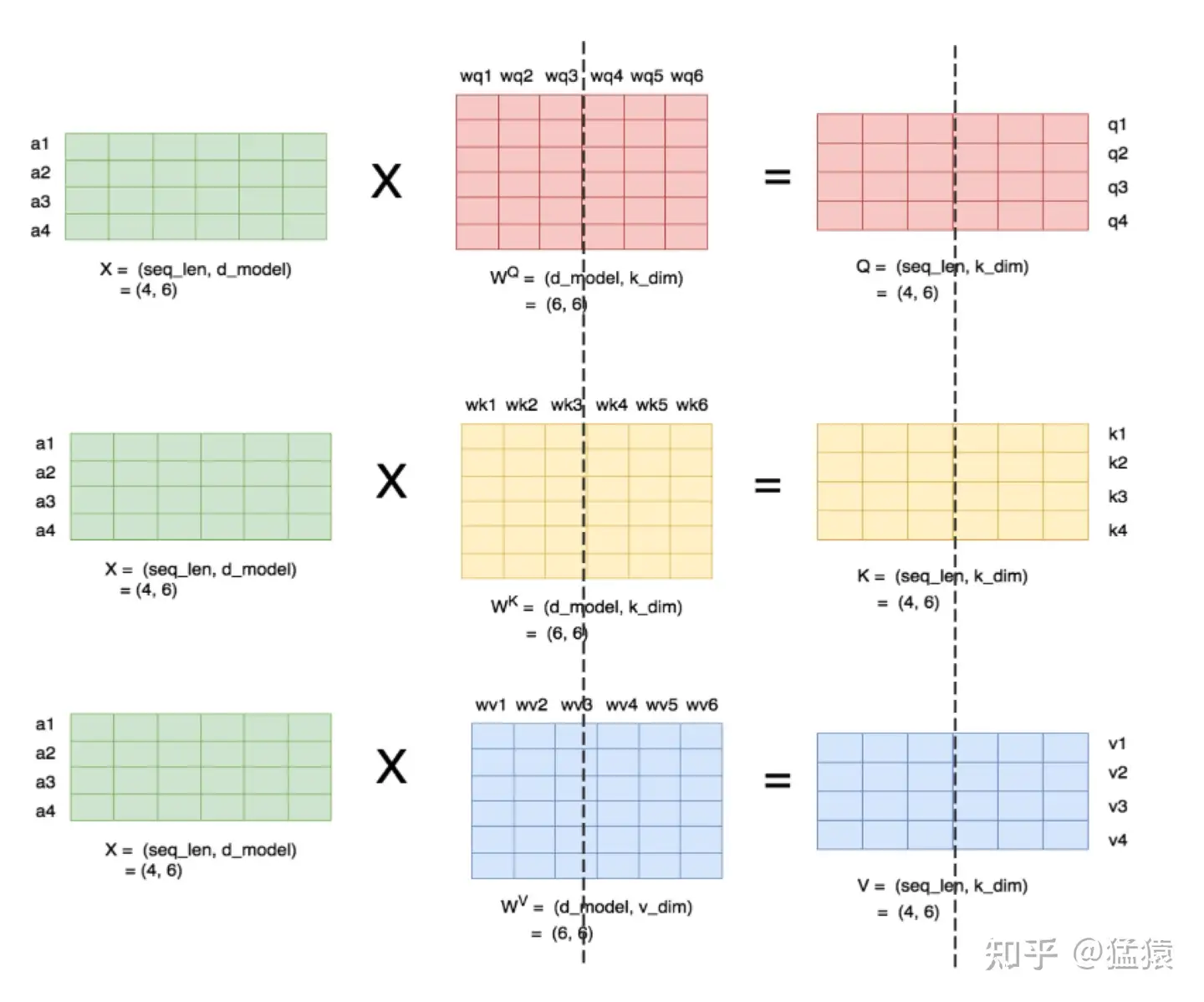
可以发现，attention的多头计算简直是为张量模型并行量身定做的，因为每个头上都可以独立计算，最后再将结果concat起来。也就是说，可以把每个头的参数放到一块GPU上。则整个过程可以画成：

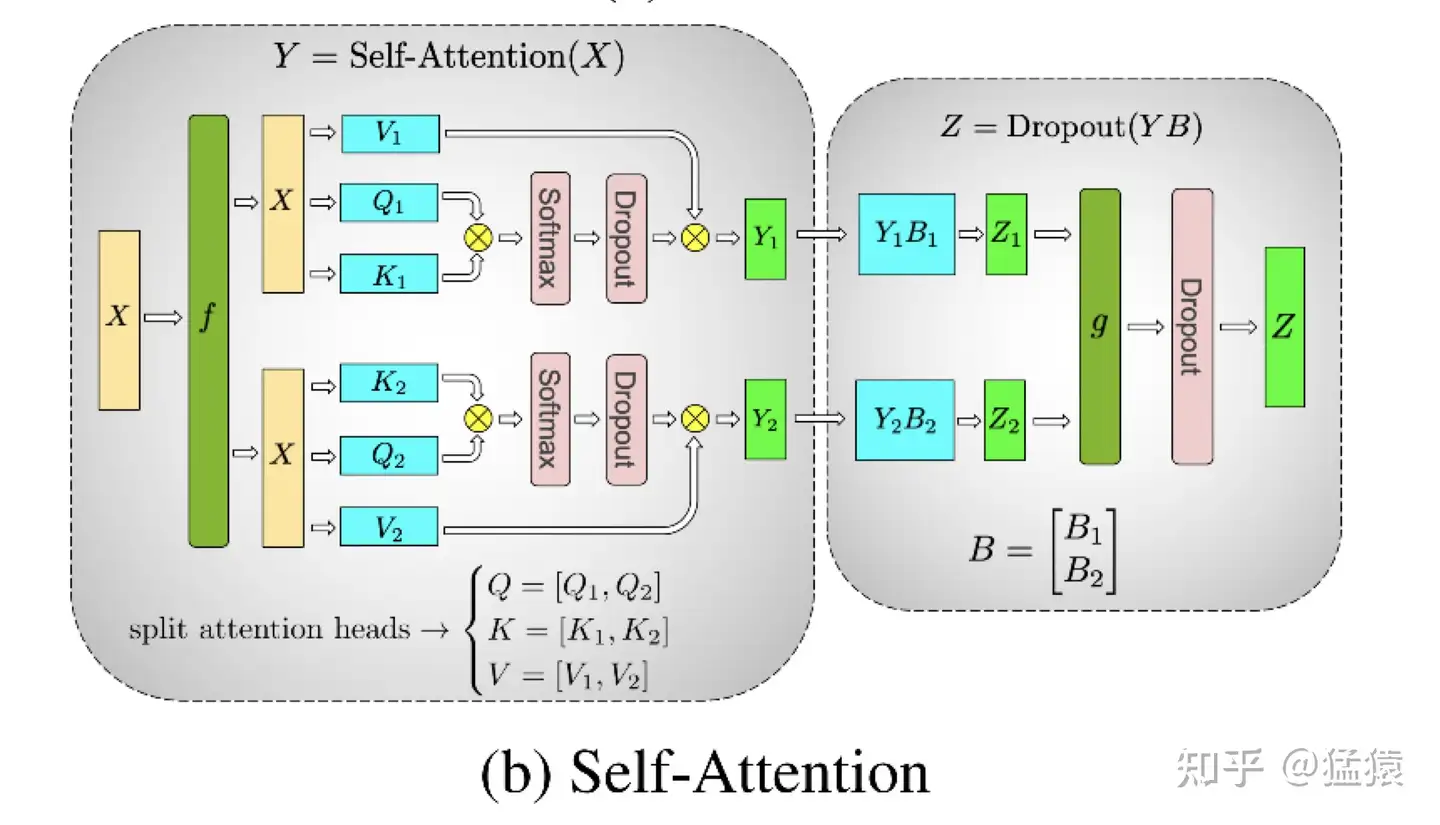
对三个参数矩阵Q，K，V，按照“列切割”，每个头放到一块GPU上，做并行计算。对线性层B，按照“行切割”。切割的方式和MLP层基本一致，其forward与backward原理也一致，这里不再赘述。
最后，在实际应用中，并不一定按照一个head占用一块GPU来切割权重，我们也可以一个多个head占用一块GPU，这依然不会改变单块GPU上独立计算的目的。所以实际设计时，我们尽量保证head总数能被GPU个数整除。

3.2 Self-Attention层的通讯量分析

类比于MLP层，self-attention层在forward中做一次AllReduce，在backward中做一次AllReduce。总通讯量也是 4Φ ，其中 Φ=𝑏∗𝑠∗ℎ

写到这里，我们可以把self-attention层拼接起来看整体的计算逻辑和通讯量：

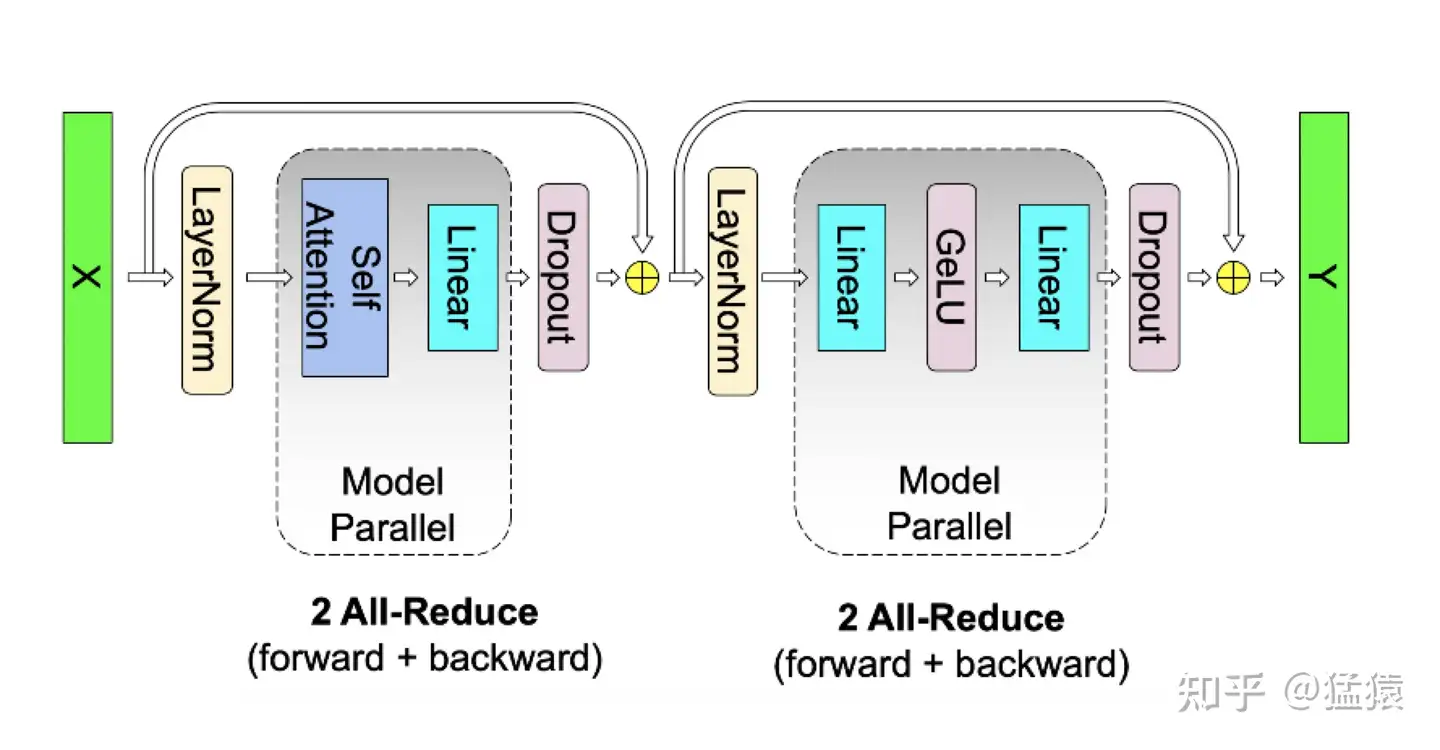
四、Embedding层

讲完了中间的计算层，现在我们来看输入和输出层。首先看来自输入层的Embeddng。

4.1 输入层Embedding

我们知道Embedding层一般由两个部分组成：

• word embedding：维度(v, h)，其中v表示词表大小。

• positional embedding：维度(max_s, h)，其中max_s表示模型允许的最大序列长度。

对positional embedding来说，max_s本身不会太长，因此每个GPU上都拷贝一份，对显存的压力也不会太大。但是对word embedding来说，词表的大小就很客观了，因此需要把word embedding拆分到各个GPU上，具体的做法如下：

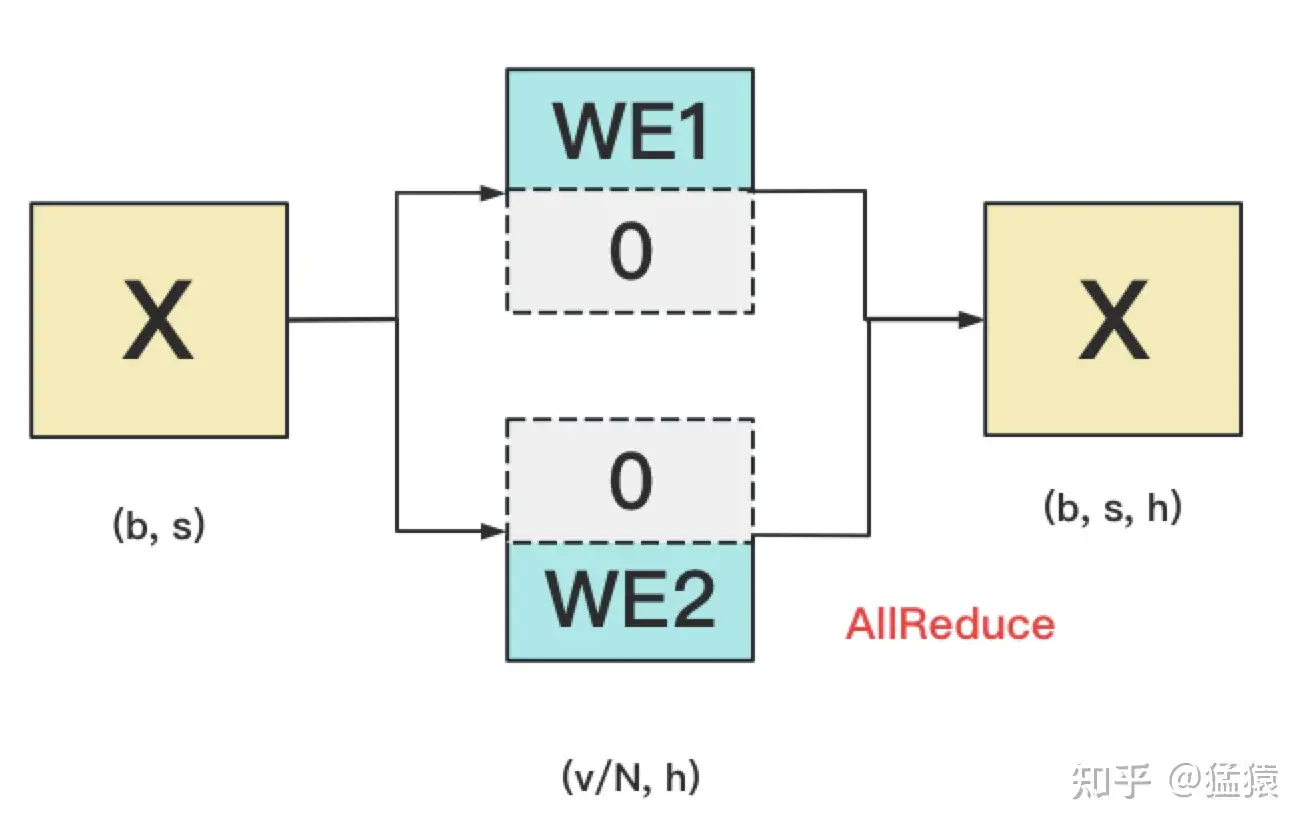
我们来详细说明下这张图。对于输入X，过word embedding的过程，就是等于用token的序号去word embedding中查找对应词向量的过程。例如，输入数据为[0, 212, 7, 9]，数据中的每一个元素代表词序号，我们要做的就是去word embedding中的0，212，7，9行去把相应的词向量找出来。

假设词表中有300个词，现在我们将word embedding拆分到两块GPU上，第一块GPU维护词表[0, 150)，第二块GPU维护词表[150, 299)。当输入X去GPU上查找时，能找到的词，就正常返回词向量，找到不到就把词向量中的全部全素都置0。按此方式查找完毕后，每块GPU上的数据做一次AllReduce，就能得到最终的输入。
例如例子中，第一块GPU的查找结果为[ok, 0, ok, ok]，第二块为[0, ok, 0, 0]，两个向量一相加，变为[ok, ok, ok, ok]

4.2 输出层Embedding

输出层中，同样有一个word embedding，把输入再映射回词表里，得到每一个位置的词。一般来说，输入层和输出层共用一个word embeding。其计算过程如下：

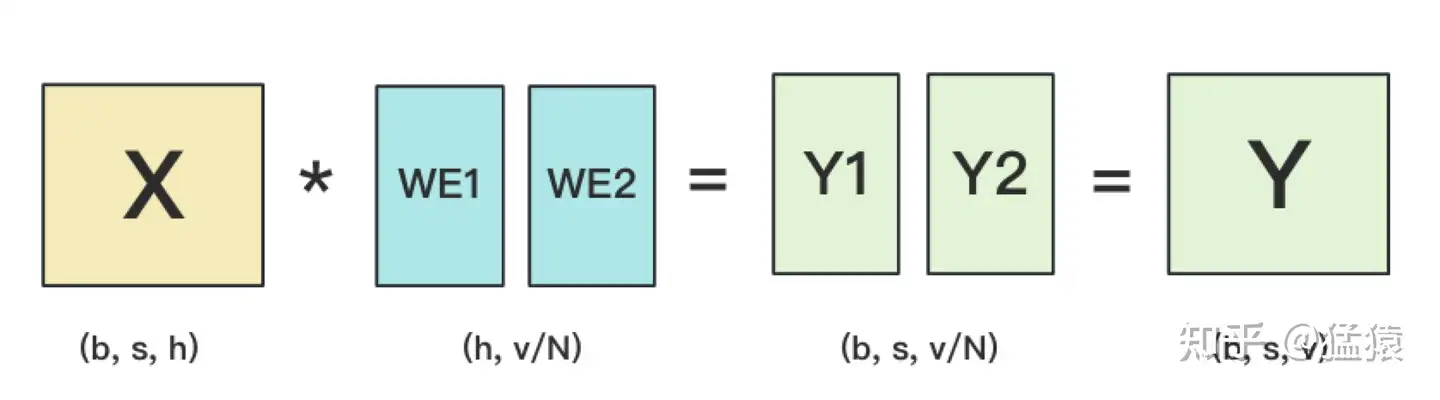
需要注意的是，我们必须时刻保证输入层和输出层共用一套word embedding。而在backward的过程中，我们在输出层时会对word embedding计算一次梯度，在输入层中还会对word embedding计算一次梯度。在用梯度做word embedding权重更新时，我们必须保证用两次梯度的总和进行更新。

当模型的输入层到输入层都在一块GPU上时（即流水线并行深度=1），我们不必担心这点（实践中大部分用Megatron做并行的项目也是这么做的）。但若模型输入层和输出层在不同的GPU上时，我们就要保证在权重更新前，两块GPU上的word embedding梯度做了一次AllReduce。现在看得有些迷糊没关系～在本系列下一篇的源码解读里，我们会来分析这一步。

五、Cross-entropy层

终于，我们来到了计算损失函数的一层。回顾一下4.2中，输出层过完embedding后的样子：

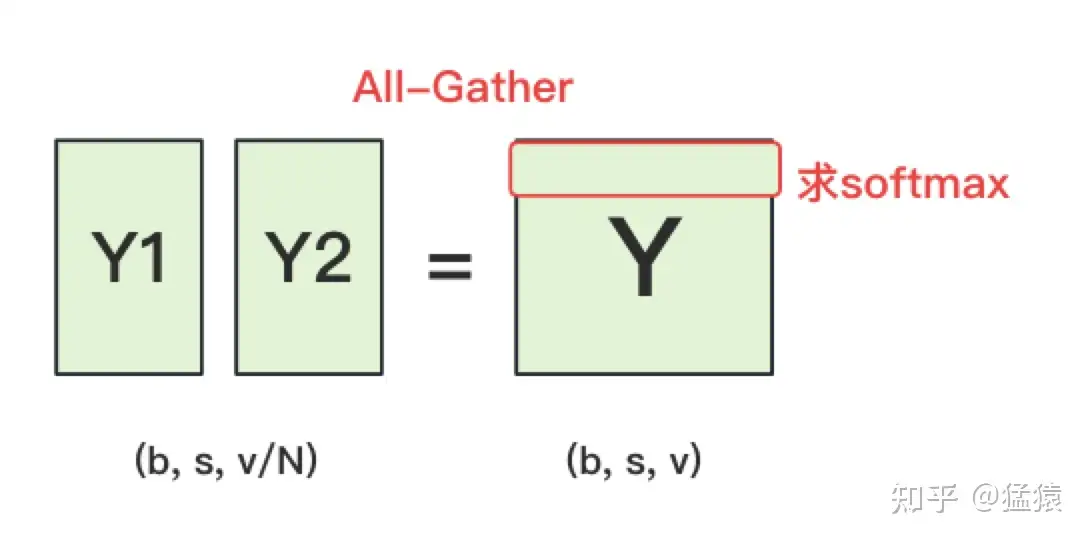
正常来说，我们需要对Y1和Y2做一次All-Gather，把它们concat起来形成Y，然后对Y的每一行做softmax，就可得到对于当前位置来说，每个词出现的概率。接着，再用此概率和真值组做cross-entropy即可。
但是All-Gather会产生额外的通讯量 𝑏∗𝑠∗𝑣 。当词表v很大时，这个通讯开销也不容忽视。针对这种情况，可以做如下优化：

• 每块GPU上，我们可以先按行求和，得到各自GPU上的GPU_sum(e)

• 将每块GPU上结果做AllReduce，得到每行最终的sum(e)，也就softmax中的分母。此时的通讯量为 𝑏∗𝑠

• 在每块GPU上，即可计算各自维护部分的e/sum(e)，将其与真值做cross-entropy，得到每行的loss，按行加总起来以后得到GPU上scalar Loss。

• 将GPU上的scalar Loss做AllReduce，得到总Loss。此时通讯量为N。

这样，我们把原先的通讯量从 𝑏∗𝑠∗𝑣 大大降至 𝑏∗𝑠+𝑁 。

⚠️⚠️关于交叉熵计算，Megatron源码中的实现方式，可能和我们理解的交叉熵有些许不同，最终的版本和图解可以参见猛猿：图解大模型训练之：Megatron源码解读2，模型并行 的第八部分。

六、张量模型并行 + 数据并行

到这里为止，我们基本把张量模型并行的计算架构说完了。在实际应用中，对Transformer类的模型，采用最经典方法是张量模型并行 + 数据并行，并在数据并行中引入ZeRO做显存优化。具体的架构如下：

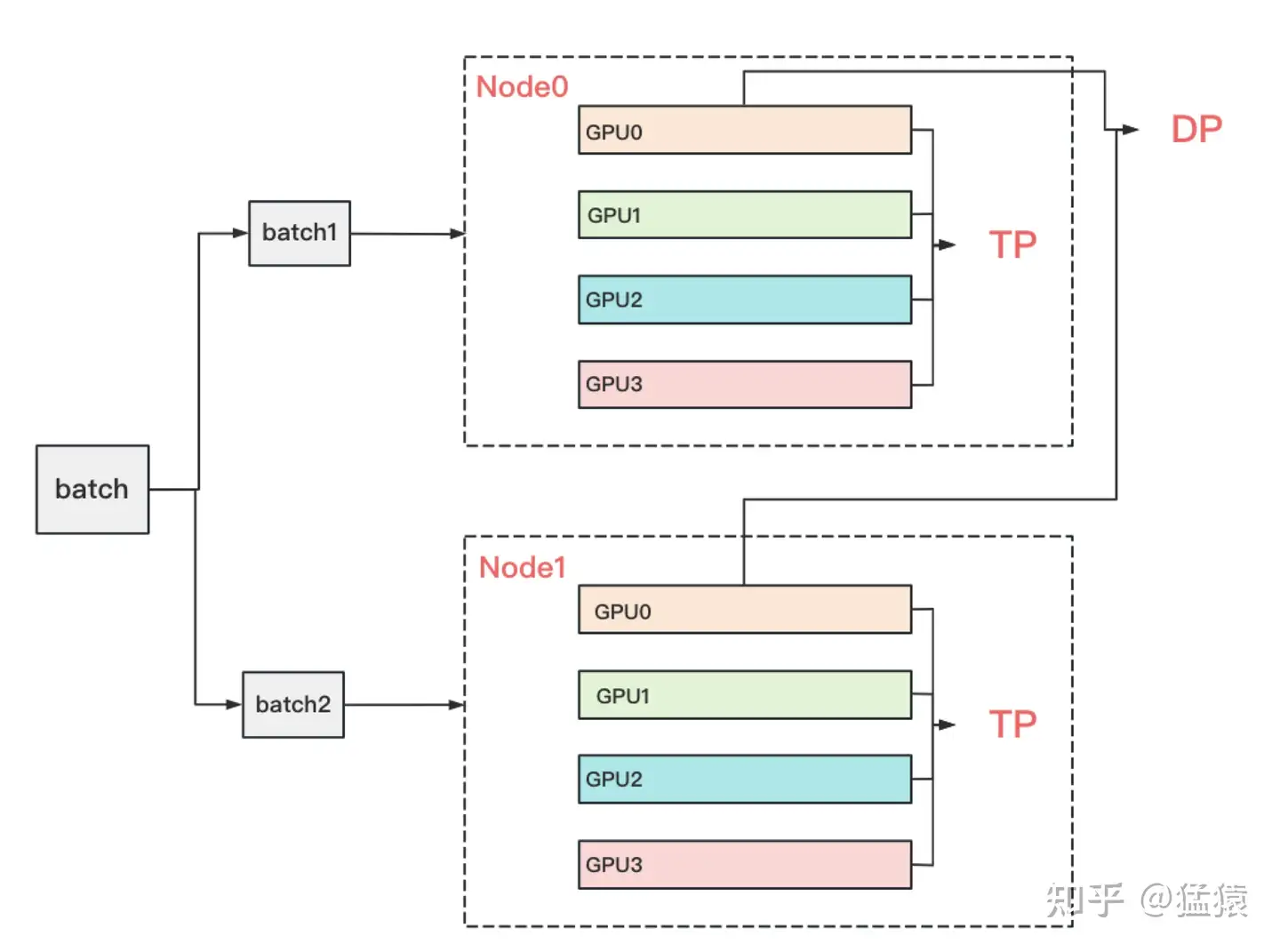
其中，node表示一台机器，一般我们在同一台机器的GPU间做张量模型并行。在不同的机器上做数据并行。图中颜色相同的部分，为一个数据并行组。凭直觉，我们可以知道这么设计大概率和两种并行方式的通讯量有关。具体来说，它与TP和DP模式下每一层的通讯量有关，也与TP和DP的backward计算方式有关。我们分别来看这两点。

6.1 TP与DP通讯量

首先，我们来分析两者的通讯量。我们关注Transformer中每一层的通讯情况。

在张量模型并行中，我们设每次通讯量为 Φ𝑇𝑃 ，从上面分析中我们知道每层做4次AllReduce，其通讯总量为 8Φ𝑇𝑃 。其中， Φ𝑇𝑃=𝑏∗𝑠∗ℎ ，则通讯总量为 8∗𝑏∗𝑠∗ℎ 。

在数据并行中，设每次通讯量为 Φ𝐷𝑃 ，从先前的文章中，我们知道每层做1次AllReduce（先不考虑ZeRO拆分权重的情况），其通讯总量为 2Φ𝐷𝑃 。其中，通讯的主要是梯度，则 Φ𝐷𝑃=ℎ∗ℎ ，总通讯量为 2∗ℎ∗ℎ 。

因此，我们要比较的就是 8∗𝑏∗𝑠∗ℎ 和 2∗ℎ∗ℎ 。忽略常数和共同项，我们最终比较的是：
[𝑏∗𝑠]𝑉𝑆[ℎ]

在实际应用中，前者可能会比后者大一些，但量级基本在 105 左右。因此，从通讯量上来说，有差异但不会显著（主要还是和模型设计相关）。不过按照常理，通讯量大的，尽量放在一台机器里（机器内的带宽大，通讯时间也会小）。通讯量相对小的，可以考虑在不同机器间做并行

6.2 TP与DP计算backward的方式

回顾上文，我们知道TP在从上一层往下一层做backward的过程中，所有GPU间需要做一次AllReduce的。例如下图：

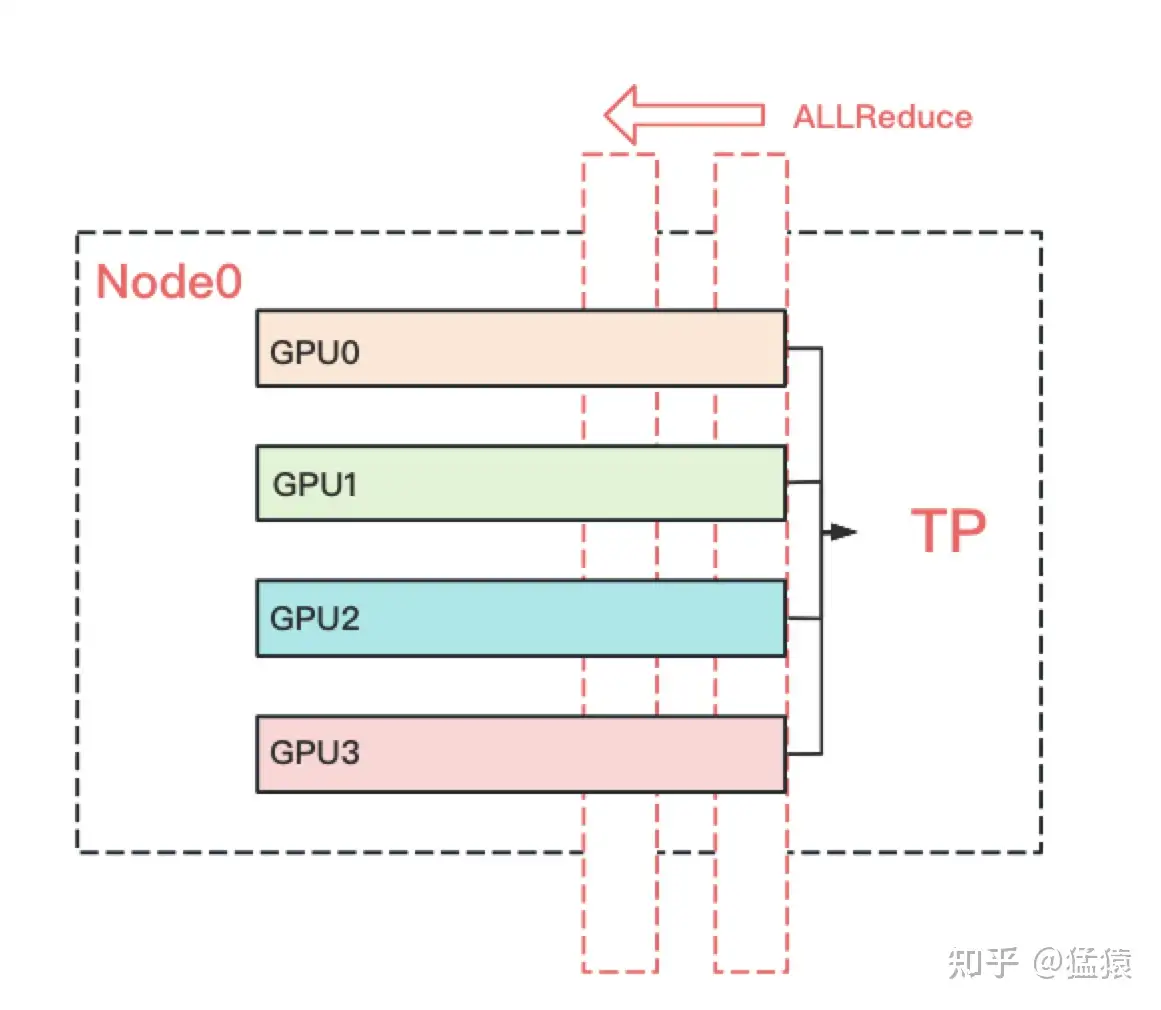
而对DP来说，本层算完梯度以后，就正常把本层的梯度发出去，和属于一个DP组的GPU做AllReduce，同时继续往下一层做backward。下一层也是同理。也就是在DP组中，下一层不依赖上一层的梯度聚合结果。因此在DP组中对带宽的要求就没那么高了。所以可以放到机器间做DP。例如下图：

七、实验效果

在讲完Megatron整体的设计后，现在我们可以更好来解读实验效果了。在原始论文中，采用32台DGX-2H，每台里有16张 Telsa V100 SXM3 32GB的GPU，总共512块GPU。在这个硬件配置上，训练不同大小的GPT2模型。核心实验数据如下：

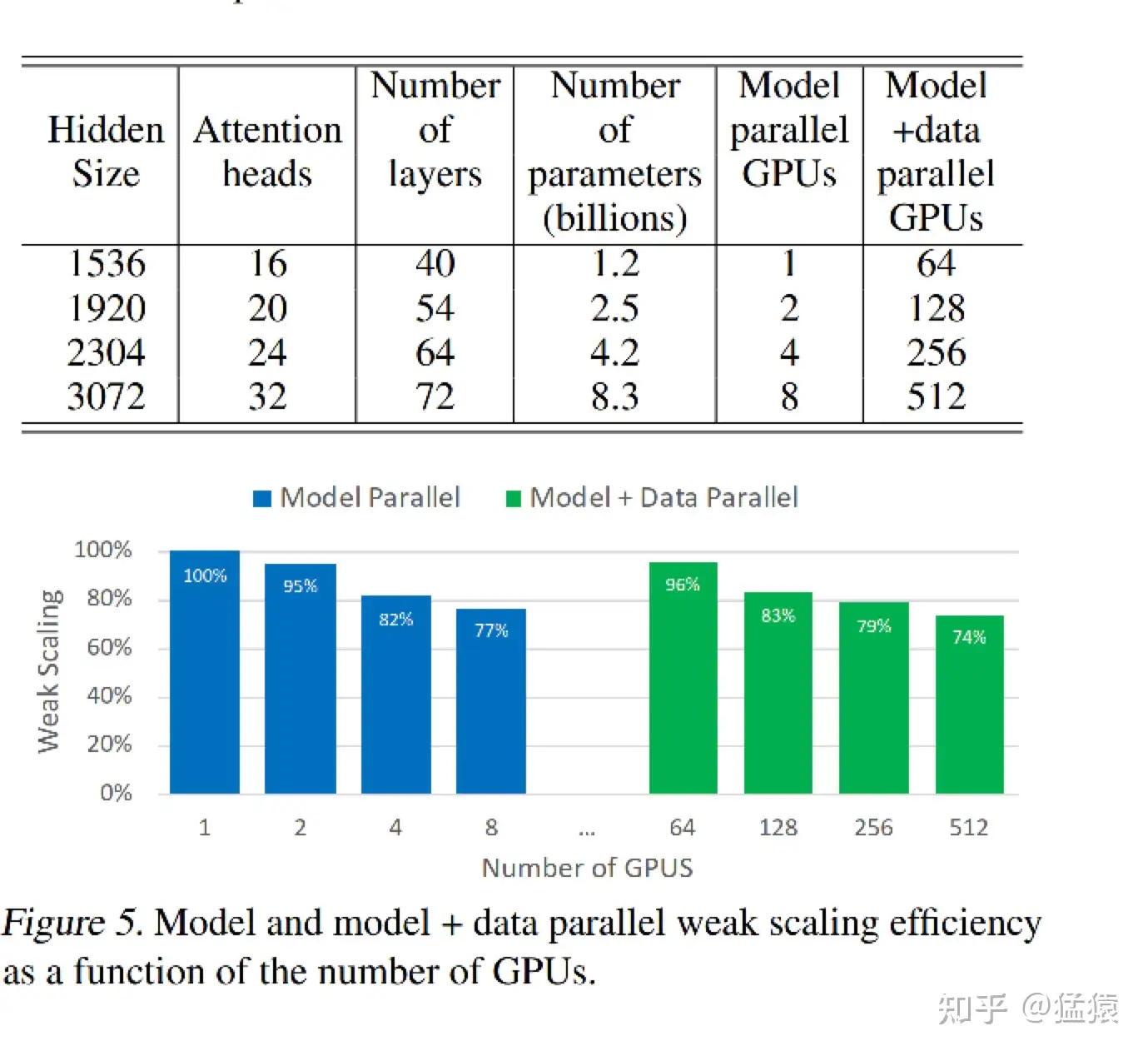
每一行表示模型的不同大小，Model parallel列表示只用TP并行时消耗的GPU卡数，其对应的单卡效率为蓝色柱状图部分。model + data parallel列表示TP + DP并行时消耗的GPU卡数，单卡计算效率为绿色柱状图部分。

7.1 纯TP实验效果

我们先来看纯TP部分。表格中的第一行是整个实验的基线，它设计了一个可以装在单卡里的GPT模型。此时不涉及卡间的通信，因此GPU的计算效率为100%。

然后，调大GPT模型到需要用2卡做TP。此时因为涉及卡间的通信，所以GPU的计算效率略有下降。从蓝色柱状图可以看出，随着模型的增大，需要的GPU数量变多，通讯量增大，单卡的计算效率是在下降的。
从1卡增加到8卡，我们可以发现需要的GPU数量和模型大小是成正比的。例如当参数量从1.2B增加到8.3B，时，需要的GPU数量也对应增加8倍。

但是，到了8以后呢？在这篇论文里，最大只做到了8卡。可是一台机器明明有16张卡，为啥不能再做到一个16B左右的模型呢？回想上一篇ZeRO部分对显存消耗的分析，当模型增大时，不仅是参数变多，还有例如activation这样的中间结果，也在占据大头显存。因此需要的GPU数量渐渐不再和模型大小成正比了。如果不引入显存优化，一台机器装不下16B的模型。

7.2 TP + DP实验效果

再来看TP + DP的结果。表格的第一行是TP + DP的基线。前面说过第一行的模型大小是可以塞进单卡里的。因此，这行中，是在每台机器中选2块GPU，一共选择64块GPU，每个GPU上都放置了一个完整的模型，GPU间做纯数据并行。其单卡计算效率为绿色柱状图第1条，96%。

在第二行中，模型大小上升，单卡已装不下完整模型。因此在每台机器中，选择4块GPU，每2块GPU组成一个TP组，因此一台机器上共2个TP组。所有机器上共64个TP组，占据128卡。这些TP组间做数据并行。以此类推模型大小再往上走时的实验配置。

不难发现，蓝色柱状图和绿色柱状图是一一对应的关系。分别表示单个模型在1卡、2卡、4卡、8卡上时的单卡效率。在引入数据并行的前提下（跨机），绿色的单卡效率并没有下降很多。这个原因我们在6.2中解释过：因为DP组内做backward计算梯度时，下一层的计算不需要依赖上一层的梯度AllReduce结果。你算你的，我发我的，对计算通讯比不会产生太大影响。

最后呢，一台DGX-2H的售价大概是40w刀，这里的硬件成本就有40 * 32 = 1280w刀。要么怎么说Megatron，注定生于NVIDIA家呢？

7.3 GPU效率计算

最后，在实验这块，咱们再来说说柱状图的weak scaling指标是怎么算出来的。毕竟在论文一开头，也摆出了一堆指标，乍一看还确实比较迷糊。

首先，在单卡装下一个模型的情况下，单GPU每秒计算量是39TeraFlOPs（可以近似理解成做矩阵乘法及加法的次数），不涉及通讯，是基线，因此计算效率为100%。

上到512卡的TP + DP后，512卡上总计每秒计算量为15100TeraFlops，因为涉及到通讯，GPU肯定不是每时每刻都在计算的，那么我们到底利用了多少GPU的算力呢？

假设512卡间无任何通讯影响，则理论算力应该为：39 * 512 = 19968TeraFlops，实际算力为15100TeraFlops。则算力利用比 = 15100/19968 = 76%。这就是文章中贯穿的76%这一指标的由来，它体现了即使做分布式训练，GPU的计算能力也不会被通信浪费掉太多，这也是Megatron的卖点之一。